BigGAN - 논문 리뷰

이번 논문은 Large Scale GAN Training for High Fidelity Natural Image Synthesis로 BigGAN이라 불리는 논문입니다.

BigGAN이란 이름에서도 Big을 쓰는만큼 나타내는 것처럼 BigGAN은 기존 GAN의 파라미터의 2~4배의 파라미터를 가지고 있으며 batchsize를 8배 이상 키운 것이 특징입니다. 이를 통해 ImageNet의 128x128 해상도에서 Inception Score(IS) Fréchet Inception Distance(FID)를 각각 166.5와 7.4로 이전 글인 SAGAN의 IS인 52.52와 FID 18.65를 넘어서는 class-conditional 이미지 합성 state of the art 모델입니다. BigGAN에 대해서 지금부터 살펴보겠습니다

소개

conditional GAN은 많은 발전을 해왔지만 SOTA 모델(SAGAN)조차 아직 실제 이미지(ImageNet)와 차이가 크며, 실제 이미지의 Inception Score인 233에 비교해 SAGAN은 52.5의 Inception Score에 그칩니다.

BigGAN은 GAN에서 생성된 이미지들과 실제 이미지인 ImageNet 간의 fidelity(품질), variety(다양성) 격차를 줄인다는 목표를 가지고 다음의 3가지를 증명합니다.

기존에 비해 2~4배 많은 수의 파라미터를 가진 모델을 사용하고 8배 이상의 큰 batch size로 모델을 학습해 GANs가 규모를 키움으로써 큰 이득을 얻는 것을 증명합니다.
orthogonal regularization과 함께 “truncation trick”을 사용해 결과 이미지의 fidelity와 variety 사이 trade-off 조절을 가능하게 합니다.
특정 대규모 GANs가 불안정한 것을 발견해 분석을 통해 새로운 기술과 기존 기술을 결합한 것이 이런 불안정을 줄일 수 있지만 학습의 안정성의 경우 성능이 제한될 때에만 달성할 수 있다는 것을 증명합니다.

위의 증명 과정을 통해 BigGAN은 class-conditional GANs를 개선해 IS, FID 모두에서 점수를 갱신합니다. ImageNet의 128x128 해상도의 경우 SOTA의 IS, FID인 52.52와 18.65를 BigGAN은 IS, FID를 166.5와 7.4로 향상시킵니다. 또한 ImageNet보다 훨씬 더 크고 복잡한 데이터셋인 JFT-300M에서도 BigGAN을 학습해 분석을 진행했습니다.

ImageNet의 128x128, 256x256, 512x512에서 학습된 모델의 가중치 값을 TF HUB에서 제공합니다.

Setting

BigGAN이 사용한 구조와 설정들은 아래와 같으며 하나씩 살펴보겠습니다.

hinge loss를 adversarial loss로 사용한 SAGAN 구조를 사용합니다.
class 정보 conditioning을 위해 Shared embedding을 사용합니다.
Exponential Weight Average를 $G$에 적용합니다.
Orthogonal Initialization / Regularization을 사용합니다.

SAGAN

BigGAN은 지난 글인 SAGAN - 논문리뷰에서 다뤘던 SAGAN이 모델 기반으로 사용됩니다. 자세한 SAGAN의 구조는 SAGAN - 논문리뷰 글을 확인해주세요:)

SAGAN과 마찬가지로 adversarial loss로 hinge loss를 사용하며 $G$와 $D$ 모두에 Spectral Normalization을 사용합니다. SAGAN에서는 G와 D의 학습 step 수를 1:1로 설정해 동일한 시간에서 더 나은 결과를 얻고자 한 것이 특징이지만 BigGAN에서는 $G$와 $D$ 학습 step 수를 1:2로 수정한 것을 사용합니다.

Conditioning

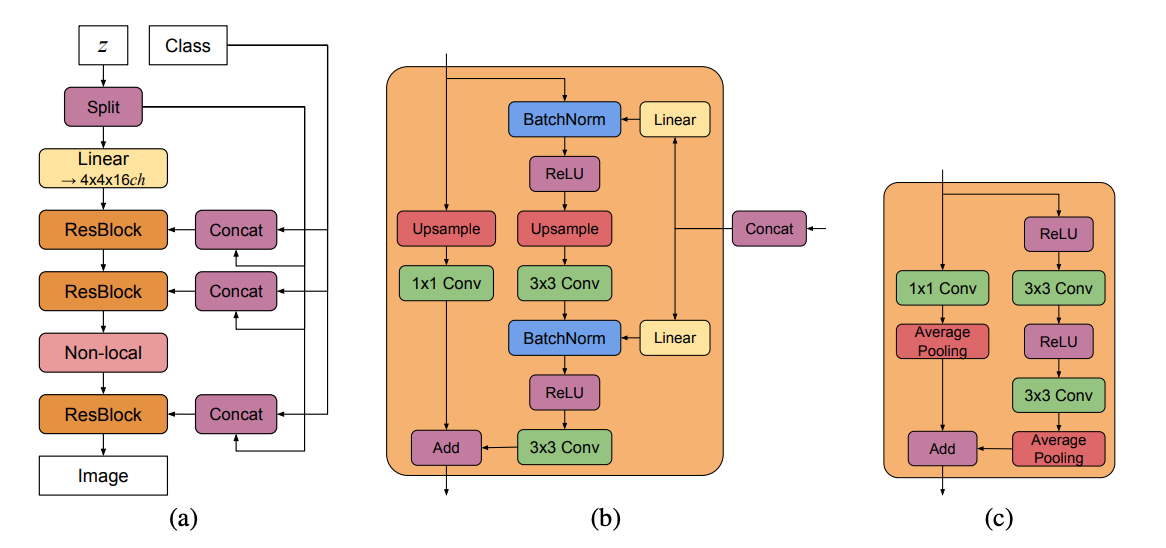
Figure 15. (a) BigGAN의 $G$의 대표적인 구조
(b) BigGAN의 $G$에 사용되는 Residual Block($ResBlock up$)
(c) BigGAN의 $D$에 사용되는 Residual Block($ResBlock down$)

BigGAN은 class 정보를 $G$와 $D$에 제공하기 위해 $G$에는 Shared embedding, hierarchical latent space를 사용하고 $D$에는 Projection Discriminator를 사용합니다.

$G$에는 single shared class embedding으로 Conditional Batch Normliazation(CBN)과 skip connection(skip-z)를 사용합니다.

$z$는 모델 입력에서 한번만 쓰이는게 일반적이지만 BigGAN은 Residual Block마다 class 정보와 함께 입력되며 Figure 15의 (a)와 (b)에서 구조를 확인할 수 있습니다. latent vector $z$가 channel 차원에 따라 동일한 크기로 분할되고 각 분할된 $z$는 shared class embedding인 CBN과 연결되어 residual block에 conditioning vector로 전달됩니다. 이 $z$가 여러 층에 전달되기에 이를 hierarchical latent space라 하고 skip connection처럼 layer를 뛰어넘어 concat되는 $z$를 skip-z라 합니다. skip-z 사용으로 약 4% 성능 향상과 함께 학습 속도 또한 18% 향상시켰다고 합니다.

$D$는 Projection Discriminator 방식을 사용합니다. Residual Block과 Scalar function을 사용해 class 정보를 사용하는 것이 특징입니다.

$G$와 $D$에 어떤 방식으로 Condition 정보를 주었는지 사용한 기술에 대해 알아보겠습니다.

Shared embedding / CBN(G)

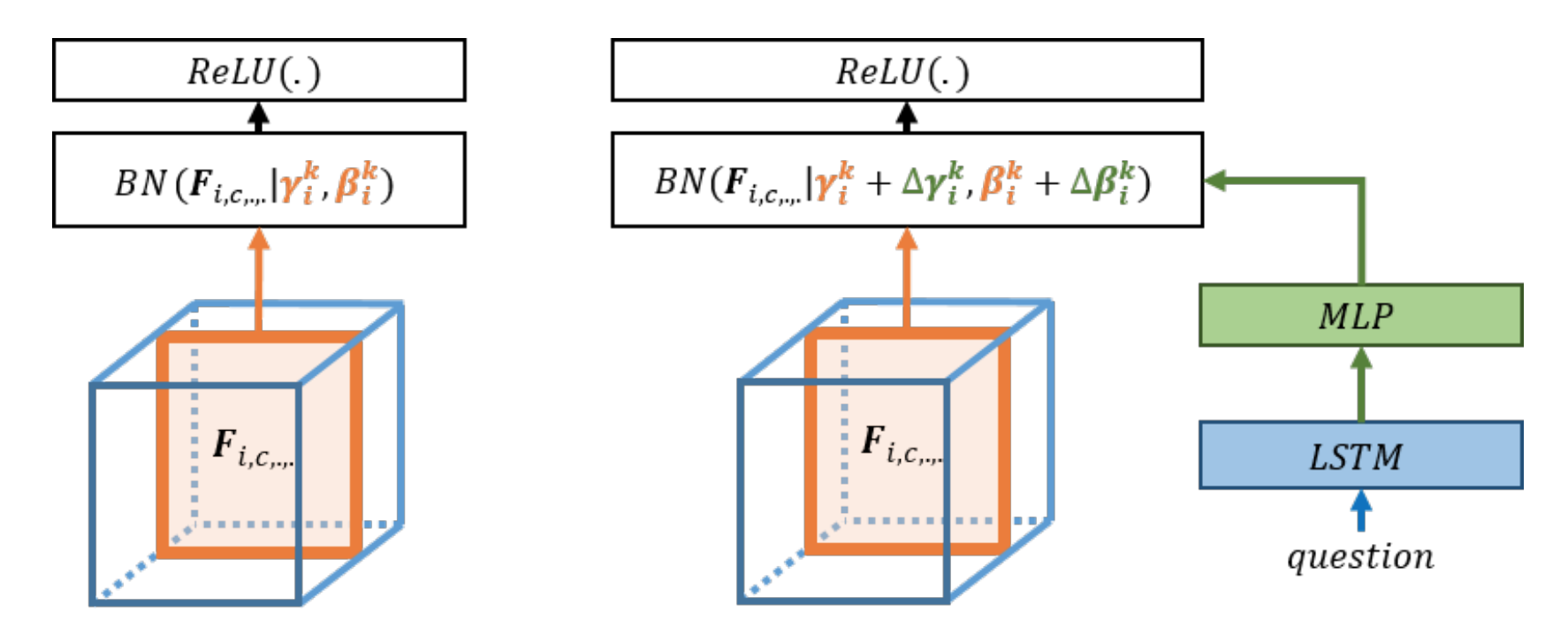
Modulating early visual processing by language의 Figure. 2
왼쪽이 일반적인 batch normalization이고 오른쪽이 conditional batch normalization의 개요를 나타냅니다.

$G$에는 Shared embedding으로 Conditional Batch Normalization(CBN) 방식을 사용합니다.

CBN은 Modulating early visual processing by language에서 소개되었으며, 기존의 Batch Normalization(BN)의 learnable parameter인 $\gamma$, $\beta$에 class 정보가 영향을 미칠 수 있도록 해 conditional 정보를 BN에 주는 방법입니다. 주고자 하는 condition에 해당하는 $e_q$를 MLP layer에 통과시켜 channel 수 마다 2개의 값 $\Delta \beta$와 $\Delta \gamma$를 계산합니다.

\[\Delta \beta = MLP(e_q) \quad \quad \Delta \gamma = MLP(e_q)\]

이후 Batch Normalization의 $\beta$, $\gamma$에 계산된 값을 더한 $\hat{\beta_c}$와 $\hat{\gamma_c}$를 Conditional Batch Normalization으로 사용합니다.

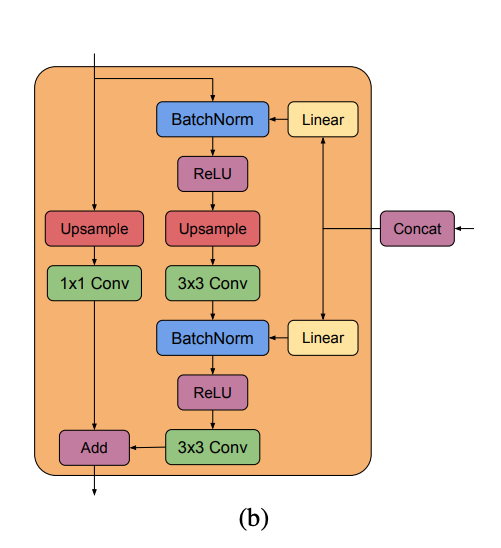
\[\hat{\beta_c} = \beta_c + \Delta \beta_c \quad \quad \hat{\gamma_c} = \gamma_c + \Delta \gamma_c\]

Figure 15. (b) BigGAN의 $G$에 사용되는 Residual Block($ResBlock up$)

Modulating early visual processing by language의 경우 VQA(Visual Question Answering) 논문으로 자연어 처리를 위해 위의 Figure 2에서 question이 LSTM과 MLP를 거쳐 $\Delta \beta$와 $\Delta \gamma$를 계산해 CBN에 사용했지만 BigGAN에서는 LSTM 없이 Linear를 사용해 $\Delta \beta$와 $\Delta \gamma$를 계산해 CBN을 사용합니다.

Projection(D)

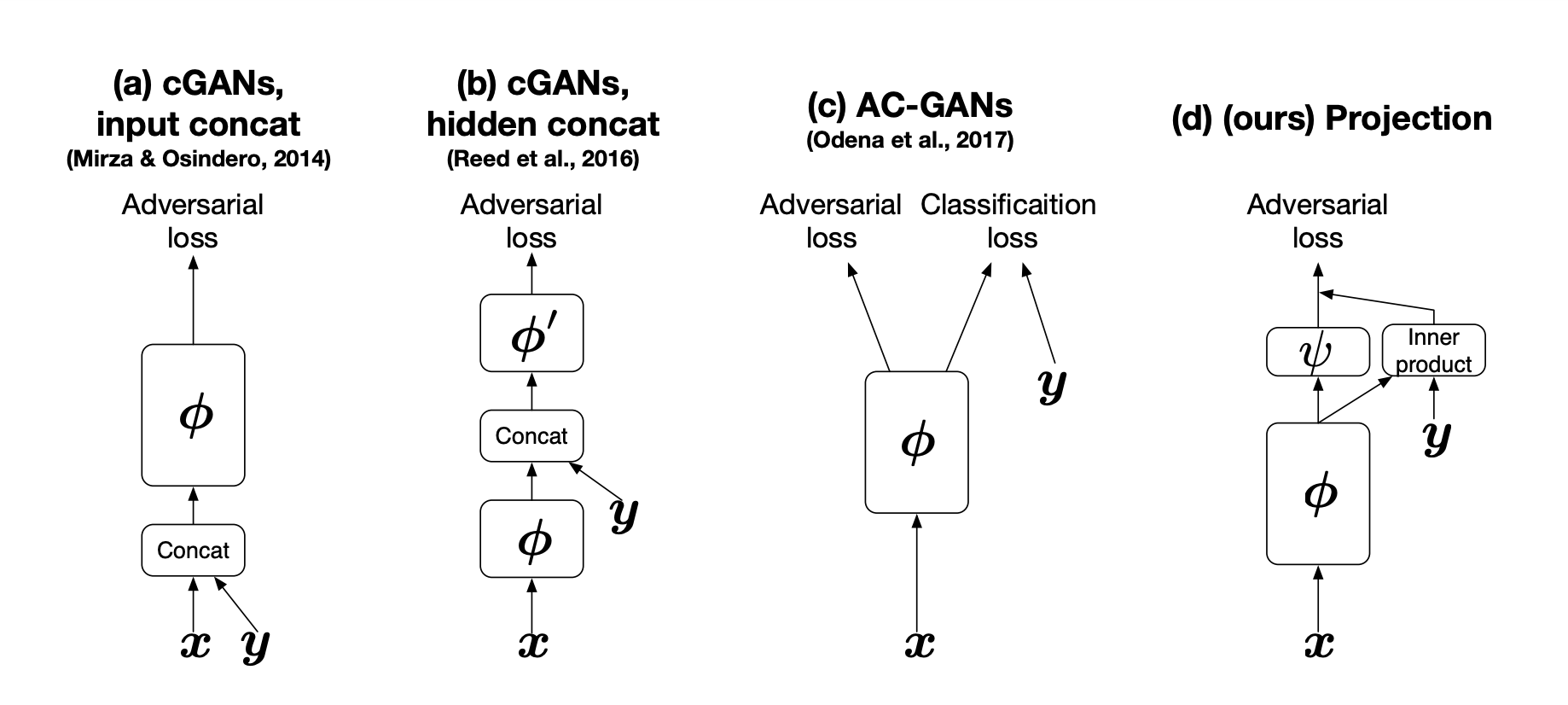
CGANS with Projection Discriminator의 Figure 1.
conditional GANs의 Discriminator 모델을 보여줍니다. 가장 우측의 모델이 BigGAN에서도 사용한 Projection Discriminator의 모양입니다.

$D$에는 Projection Discriminator를 사용합니다.

cGANs with Projection Discriminator에서 제안한 모델로 GAN의 Discriminator에서 conditional 정보를 다루는 방법들이 발전해온 구조를 묘사한 위의 Figure의 (d)에 해당하며 수식으로 아래와 같이 나타낼 수 있습니다.

\[f(x, y; \theta) := f_1(x, y:\theta) + f_2(x;\theta) = y^T V \phi(x; \theta_{\Phi}) + \psi(\phi(x; \theta_{\Phi}); \theta_{\Psi})\]

$\phi$는 BigGAN에서 Residual network를 사용하며 $\psi$은 $\phi$와 연결되는 scalar function으로 입력된 이미지가 진짜인지 가짜인지 판별하는 함수로 이미지 판별 결과 값 하나를 출력하기 때문에 scalar function입니다.

수식으로는 복잡해 보이지만 $\psi(\phi(x; \theta_{\Phi}); \theta_{\Psi}) $는 Residual network $\phi$ 에 이미지 $x$를 입력하고 결과 값을 activation(scalar function) $\psi$ 에 연결해 이미지가 진짜인지 가짜인지 판별한 값으로 지금까지 사용한 판별모델과 같은 구조입니다.

$V$는 $y$의 embedding matrix로 $y^T V$가 Figure의 (d)에서 $y$가 입력되는 부분을 의미합니다. Residual network $\phi$에 $x$가 입력되었을 때의 feature map이 두 갈래로 나뉘어 하나는 activation(scalar function)인 $\psi$로 입력되고 다른 한 갈래는 condition에 해당하는 $y$의 embedding과 계산되어 이후 두 갈래로 나눠져 계산된 값들이 합쳐져 결과로 출력됩니다.

대략적인 흐름을 이해하는 데 도움이 될 것 같아 github에 있는 코드를 아래에 가져왔습니다.

class SNResNetProjectionDiscriminator(chainer.Chain):
    def __init__(self, ch=64, n_classes=0, activation=F.relu):
        super(SNResNetProjectionDiscriminator, self).__init__()
        self.activation = activation
        initializer = chainer.initializers.GlorotUniform()
        with self.init_scope():
            self.block1 = OptimizedBlock(3, ch)
            self.block2 = Block(ch, ch * 2, activation=activation, downsample=True)
            self.block3 = Block(ch * 2, ch * 4, activation=activation, downsample=True)
            self.block4 = Block(ch * 4, ch * 8, activation=activation, downsample=True)
            self.block5 = Block(ch * 8, ch * 16, activation=activation, downsample=True)
            self.block6 = Block(ch * 16, ch * 16, activation=activation, downsample=False)
            self.l7 = SNLinear(ch * 16, 1, initialW=initializer)
            if n_classes > 0:
                self.l_y = SNEmbedID(n_classes, ch * 16, initialW=initializer)

    def __call__(self, x, y=None):
        h = x
        h = self.block1(h)
        h = self.block2(h)
        h = self.block3(h)
        h = self.block4(h)
        h = self.block5(h)
        h = self.block6(h)
        h = self.activation(h)
        h = F.sum(h, axis=(2, 3))  # Global pooling
        output = self.l7(h)
        if y is not None:
            w_y = self.l_y(y)
            output += F.sum(w_y * h, axis=1, keepdims=True)
        return output

EMA(EWA)

$G$의 weight에 moving average를 사용하는데, PGGAN, ProGAN이라 불리는 Progressive Growing of GANs for Improved Quality, Stability, and Variation에서 사용한 것으로 원 논문에서는 learning rate를 decay하도록 따로 설정하지는 않지만 $G$의 출력을 시각화하기 위해 Exponential Weight Average(Exponential Moving Average)를 사용한다고 합니다.

Exponential Weight Average는 지금까지 계산된 weight를 모두 사용해 weight를 업데이트하는 방법으로 가장 최신의 weight의 가중치를 더 크게 반영하고 오래된 weight의 영향을 감소시키기 위해 이전의 weight들은 iteration이 반복될 때마다 decay이 곱해져 축적됩니다. BigGAN에서는 decay 값으로 0.999가 사용되며 축적된 weight의 average 값이 가중치로 사용됩니다.

Orthogonal

Initialization

논문에서는 $N(0, 0.2I)$ 또는 Xavier initialization이 아닌 orthogonal initialization을 사용했다고 합니다. Orthogonal initialization은 Exact solutions to the nonlinear dynamics of learning in deep linear neural networks에서 사용된 방법으로 random weight를 svd를 통해 얻은 orthogonal matrix를 initial weight로 사용하는 방법입니다.

W = np.random.randn(ndim, ndim)
u, s, v = np.linalg.svd(W)

u -> initiliazatin matrix로 사용

참고

ILHO AHN / Weight Initializer 종류

Regularization

대부분의 이전 연구들은 $z$를 $N(0, I)$ 또는 $U[-1, 1]$에서 선택해 사용했습니다. 저자들은 latent space로 기존에 사용하던 latent가 아닌 대안이 될 수 있는 다른 latent들을 실험했습니다(논문의 Appendix E에서 실험한 latent 목록을 확인할 수 있습니다).

SAGAN을 기준으로 $z \sim N(0, I)$에서 다른 latent를 사용했을 때 가장 잘 작동하는 2개의 latent는 Bernoulli ${ 0, 1 }$와 Censored Normal max($N(0, I), 0$)로 두 가지 모두 학습 속도를 향상시키고 최종 성능을 약간 향상시켰다고 합니다.

또한 새로운 trick으로 variety와 fidelity를 조절하며 IS와 FID 점수를 향상시킬 수 있는 truncation trick을 발견합니다. train 과정에서는 $z \sim N(0, I)$를 그대로 사용해 이전의 모델들과 같은 방법이지만, evaluate 시 $z$ 값이 threshold 값을 넘어가게 된다면 다시 추출하는 것이 truncation trick 입니다.

Figure 2. (a) truncation 증가에 대한 효과. 왼쪽에서 오른쪽으로 threshold 2, 1, 0.5, 0.04로 설정되었습니다.
(b)truncation을 적용해 상태가 좋지 않은 모델의 Saturation artifacts

Truncation trick은 설정한 threshold 값에 따라 결과 이미지의 fidelity와 variety를 조절할 수 있는 방법입니다. Figure 2 (a)에서 threshold 값이 큰 좌측의 결과 이미지들은 다양한 이미지가 출력되나 상대적으로 품질이 떨어지며(fideliyty $\downarrow$, variety $\uparrow$), threshold 값이 작아지며 우측으로 갈수록 결과 이미지들의 다양성은 떨어지나 품질이 올라가는 것(fideliyty $\uparrow$, variety $\downarrow$)을 볼 수 있습니다.

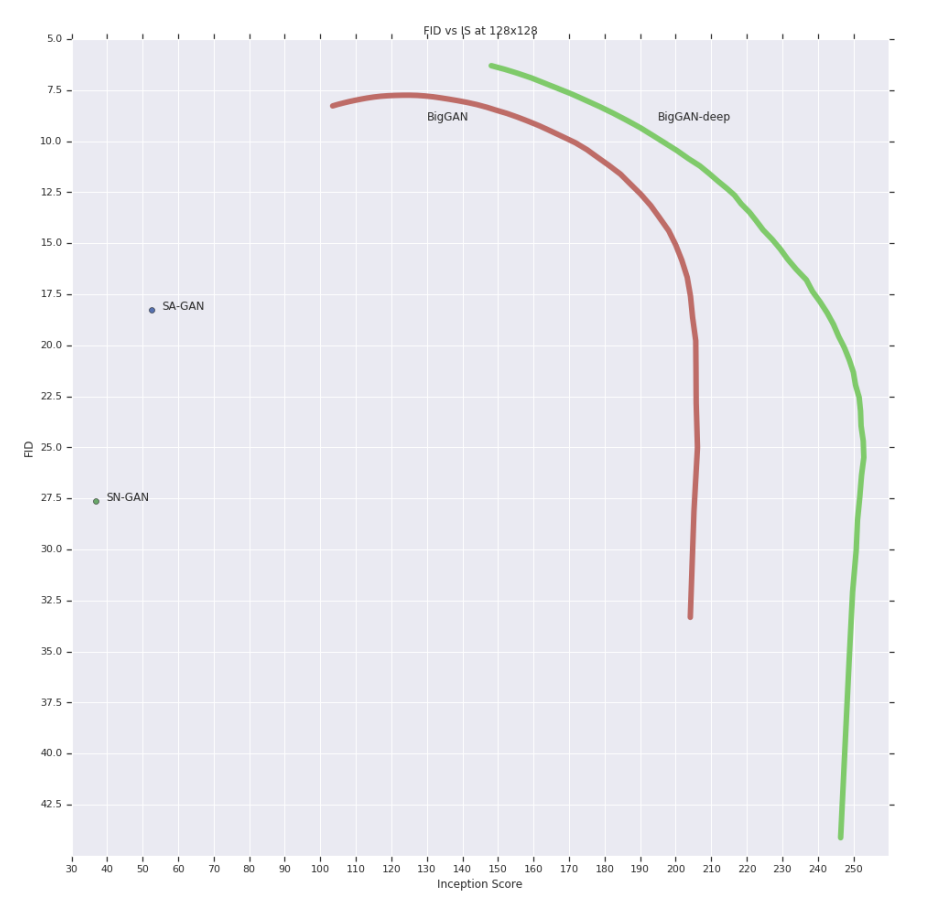
Figure 17. 128x128 해상도에서 IS vs FID

Truncation trick을 사용해 variety-fidelity를 연상시킬 수 있는 precision-recall 곡선인 Figure 17을 만들 수 있습니다.

IS 점수는 클래스 condition의 다양성(variety)에 불이익을 주지 않기 때문에 truncation threshold 값을 줄이면 IS 점수가 증가해 precision과 유사합니다. 반대로 FID는 recall과 유사해 다양성이 부족한 것에는 불이익을 주기 때문에 truncation이 0에 가까워지고 다양성이 감소함에 따라 FID 점수가 급격이 감소합니다.

많은 모델들에서 학습에서 사용한 latent와 다른 분포에서 추출한 $z$를 사용하는 것이 문제가 되기 때문에, 일부 모델은 truncation에 적합하지 않으며 truncation된 $z$를 입력했을 때 Figure 2 (b)에서 볼 수 있는 saturation artifact를 생성합니다. 이를 해결하기 위해 저자는 $G$를 smooth하게 조절해 truncation에 대한 적응성을 강화해 truncated $z$가 좋은 결과에 매핑되도록 orthogonal regularization을 도입합니다.

사실 orthogonal regularization은 BigGAN 저자의 이전 논문인 Neural Photo Editing with Introspective Adversarial Networks에서 제안되었습니다.

\[R_{\beta}(W) = \beta \| W^{\top} W -I \|^2_F\]

$W$는 weight matrix이고 $\beta$가 hyperparameter로 weight를 orthogonal하게 제한하도록 orthogonal regularization이 제안되었으나, spectral normalization 논문에서 orthogonal regularization은 중요한 singular value에 상관 없이 모든 singular value를 1로 설정하기 때문에 spectrum 정보를 파괴하는 문제가 있다고 지적을 당해 BigGAN 논문에서는 변형된 아래의 버전을 사용합니다.

\[R_{\beta}(W) = \beta \|W^{\top}W \odot(1-I) \|^2_F\]

$1$은 모든 요소가 $1$로 설정된 행렬이며, $\beta$를 $10^{-4}$로 설정해 모델이 truncation에 적응할 수 있도록 likelihood를 개선할 수 있다는 것을 찾게되었고, orthogonal regularization을 사용한다면 16%의 경우에만 truncation trick을 적용할 수 있었던 것을 60%까지 적용할 수 있게 되었다고 합니다.

추가로 truncation 없이 가장 잘 작동하는 2개의 latent는 Bernoulli ${ 0, 1 }$와 Censored Normal max($N(0, I), 0$)는 학습 속도와 성능 모두를 향상시켰지만 truncation과 함께 적용하는 것에는 적합하지 않았다고 합니다.

참고

Young Seok Kim / PR-109: Large Scale GAN Training for High Fidelity Natural Image Synthesis

Scaling Up GANs

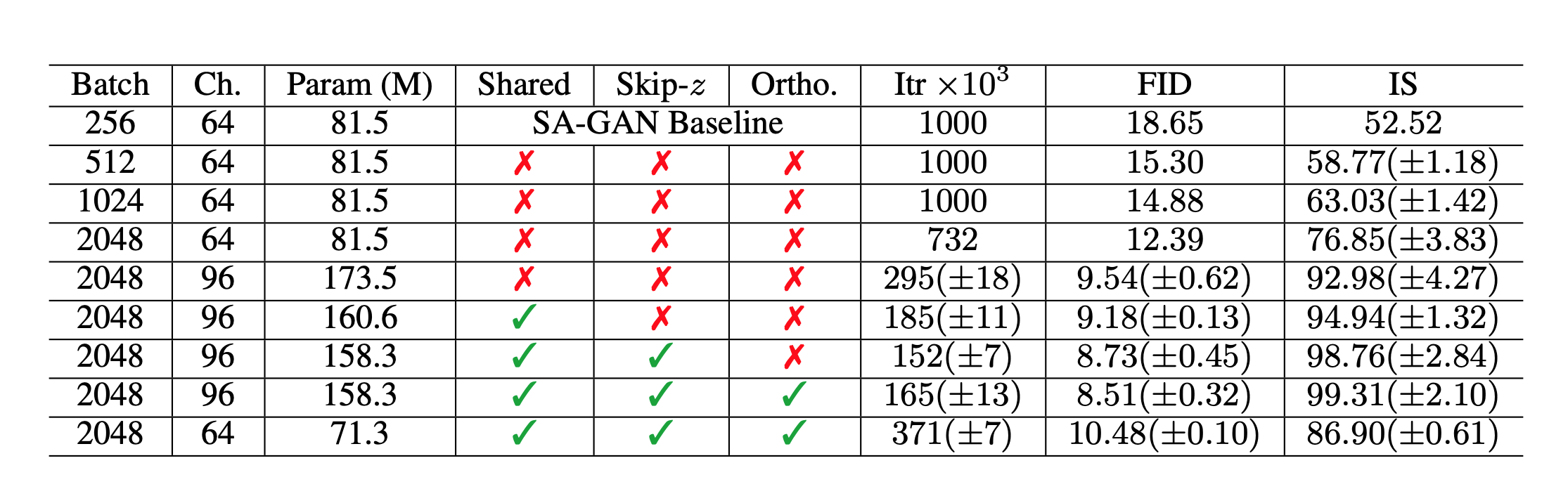
Table 1. ablation 실험을 위한 Fréchet Inception Distance(FID, 낮은 점수가 더 좋음)와 Inception Score(IS, 높은 점수가 더 좋음).
Batch는 batch size, Param은 parameter의 수, CH는 각 계층의 단위 수를 나타내는 channel의 수, Shared는 shared embedding의 사용 여부, Skip-z는 잠재 계층에서 다른 계층으로의 skip connection 사용 여부, Ortho.는 Orthogonal Regularization, Itr는 1000이라면 $10^6$ iteration까지 안정적이며, 그 외에는 해당 iteration에서 붕괴(collapse)되었다는 것을 나타냅니다.
1 ~ 4행 외에는 8번의 random initialization에 걸쳐 결과가 계산됩니다.

지금까지 BigGAN이 사용한 기술들과 설정에 대해 보았다면 이번에는 BigGAN이 SAGAN을 baseline 모델로 설정해 규모를 키워 얼마만큼 성능을 향상시켰는지 살펴보겠습니다.

Table 1의 1~4행은 단순히 batch size를 최대 8배까지 증가시키는 것으로 IS 점수는 sota에서 46% 향상됨을 보여줍니다. 또한 channel 수를 50% 증가시켜 파라미터 수를 약 2배로 늘려 IS가 21% 더 개선되었습니다. 깊이를 2배로 늘리는 것은 처음엔 개선으로 이어지지 않았지만 residual block 구조를 사용하는 BigGAN-deep 모델에서 해결되었다고 합니다.

이런 scale up으로 인한 주목할 만한 부작용은 training collapse입니다. BigGAN은 불안정해지거나 training collapse를 겪기 때문에 Table 1에 표시된 성능은 collapse 직전에 저장된 checkpoint의 점수입니다.

Collapse

BigGAN은 대규모 모델 사용과 대규모 batch 학습으로 기존 state of the art를 개선했지만 training collapse를 겪기 때문에 조기 중단(early stopping) 실행을 필요로 합니다.

BigGAN의 저자들은 이전 논문들에서는 안정적이였던 설정들이 BigGAN과 같은 대규모 모델에 적용될 때 불안정해지는 이유를 G와 D의 weight spectra를 분석해 모델의 collapse 원인에 대해 분석하며 weight의 singular value에서 패턴을 찾을 수 있었습니다.

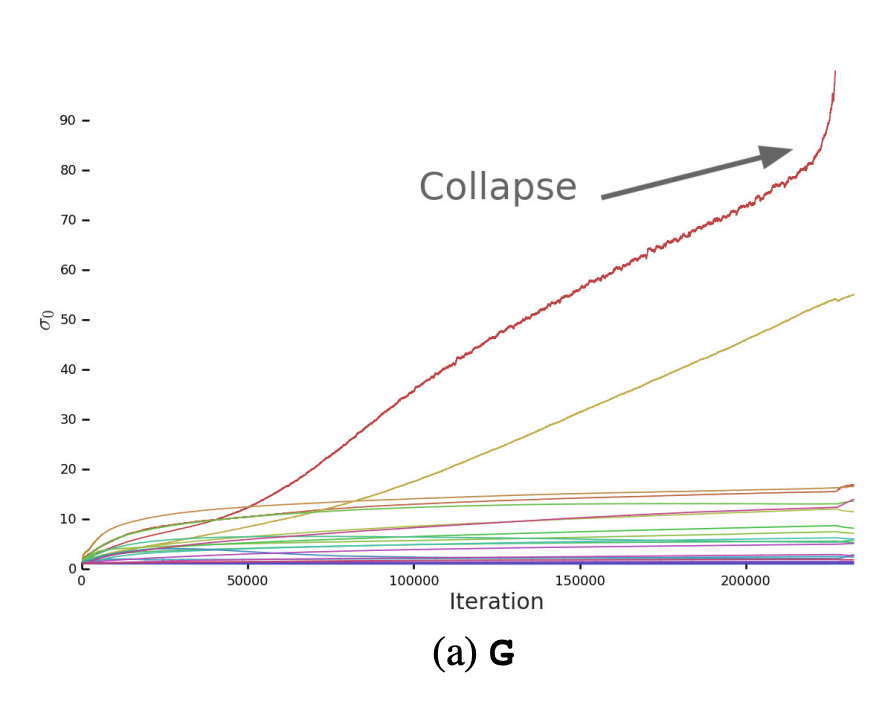
Figure 3. (a) Spectral Normalization 전 $G$ layer들의 첫번째 single value $\sigma_0$의 plot
$G$의 대부분의 layer들은 잘 작동하는 spectrum들을 가지고 있지만, 제약이 없는 경우 일부가 학습 내내 값이 상승하고 collapse 시 값이 폭발합니다.

$G$의 경우 일부 layer의 weight 행렬의 singular values $\sigma$ 값이 학습 내내 상승하고 collapse 될 때 폭발하는 spectrum들을 가지고 있었습니다. 이를 방지하기 위해 $G$에 추가 조건을 부과해 폭발하는 spectrum을 막아 training collapse를 방지하고자 했으나 Spectral Normalization을 사용하더라도 일부의 경우 성능이 약간 개선되기만 할 뿐 training collapse를 막지 못했다고 합니다.

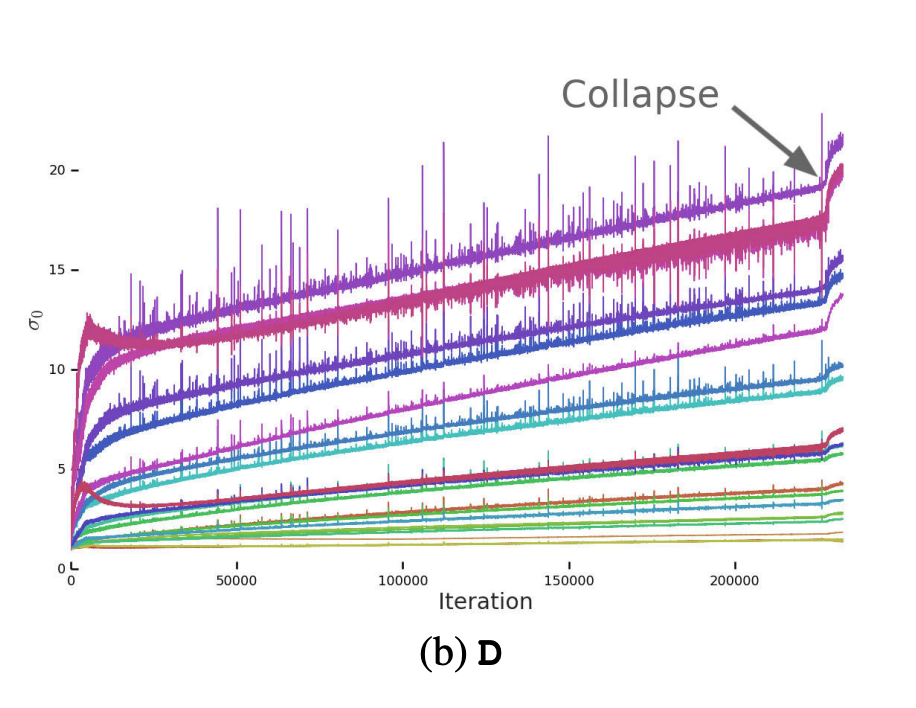
Figure 3. (b) Spectral Normalization 전 $G$ layer들의 첫번째 single value $\sigma_0$의 plot
$D$의 spectrum들은 noise가 있지만 더 잘 작동합니다.

$G$에서 안정성을 보장하지 못한다면 $D$에서 안정성을 보장할 수 있는지 확인해야 합니다. $G$와 마찬가지로 $D$의 spectrum들을 조사한 결과 $G$와 달리 spectrum들이 noisy하고 singular value가 학습 내내 증가하지만 폭발하지는 않으며 collapse 시에만 값이 뛰는 것을 관찰하게 됩니다.

$D$의 Frobenius norm이 매우 smooth하다는 것을 발견해 $D$의 Jacobian 변화를 regularize하는 gradient penalty를 사용하며, Which Training Methods for GANs do actually Converge?에서 사용한 R1 zero-cetered gradient penalty를 사용합니다.

\[R_1 := \frac{\gamma}{2} \mathbb{E} _{p \mathcal{D}(x)}[\| \nabla D(x) \|^2_F]\]

논문에서 제안된 $\gamma$ 강도 10으로 학습을 하면 안정적이지만 성능이 심각하게 저하되어 IS가 45% 감소했다고 합니다. penalty를 줄이면 성능 감소는 완화되지만 안정되었던 spectrum들이 다시 불안정해지며 penalty 강도로 갑작스러운 collapse가 발생하지 않는 최저 강도인 1로 설정할 경우 IS는 20% 감소합니다.

collapse를 방지하기 위해 $D$에게 높은 penalty를 주는 것으로 안정성을 강제할 수 있지만 성능이 떨어지는 것을 확인했지만 다양한 collapse 방지를 위한 기술들을 사용해 collapse를 미뤄 더 나은 성능을 달성하기 위한 방법 또한 제시합니다.

Collapse 방지 실험

collapse의 증상으로 갑작스럽게 발생해 수 백번 iteration 내에 최고치의 결과 품질이 최저치로 떨어지는 현상이 발생한다고 합니다. $G$의 singular value가 갑작스럽게 커질 때 collapse를 감지할 수 있지만 singular value가 특정 값(threshold) 이상이 될 때 collapse하는 것은 아니기 때문에 모델이 collapse되기 1~2만 iteration의 모델 checkpoint에서 일부 hyperparameter를 수정해 collapse를 방지하거나 지연시킬 수 있는지에 대한 실험들을 진행했으며 내용은 아래와 같습니다.

$G$, $D$, $G$&$D$의 learning rate를 초기 값에 비해 높이면 즉각적인 collapse가 발생합니다. 초기 learning rate로 설정했을 때 문제 없던 값으로 변경했을 때도 collapse가 발생했습니다.
$G$의 learning rate를 줄이되 $D$의 learning rate를 그대로 유지하면 경우에 따라 10만 iteration 이상 collapse를 지연시킬 수 있으나 학습이 실패할 가능성이 있었습니다. 반대로 $G$의 learning rate를 유지하면서 $D$의 learning rate를 낮추면 즉각적인 collapse로 이어졌습니다. 저자들은 $D$의 learning rate를 줄이는 것이 $D$가 $G$를 따라잡을 수 없어(keep up) 학습이 collapse 된다고 생각해 $G$와 $D$ 학습 step 수를 조절했지만 영향을 미치지 않거나 collapse를 지연시키며 학습이 실패했다고 합니다.
collapse 전 $D$를 freeze되면 $G$는 즉시 collapse 되어 loss가 300 이상의 값으로 뛰며, 반대로 $G$를 freeze 시키면 $D$가 안정적으로 유지되며 loss가 0으로 천천히 감소되었습니다. $D$가 안정적이기 위해 $G$에게 최적으로 유지되어야 하는데 $G$가 이 minmax 게임에서 이기게 되는 것($D$를 freeze하는 것)은 학습이 완전하게 collapse되었습니다.

추가적인 collase 실험으로 $G$와 $D$의 minmax game인 GAN에서 $G$의 conditioning이나 최적화 설정과는 관계없이 $G$가 $D$를 이길 수 있게 되는 결과는 학습 과정에서 완전한 collapse라는 것과 $D$를 $G$에 비해 더 많은 step으로 학습하는 것은 $D$가 잘 학습되더라도 안정성을 보장하기에는 부족하다는 결론으로 이어졌습니다.

이에 대해 $D$의 spectrum을 추가 연구해 gradient, hinge loss의 margin 크기, 모델의 memorization과 관련되어 여러 hyperparameter를 조절해 실험했지만 안정적이지 않거나 성능이 하락하는 것을 초래했다고 합니다.

결과

Figure 4. truncation threshold 0.5(a, b, c)로 생성한 BigGAN의 결과들과 class leakage 예시(d)

Table 1의 8행 설정(Batch size:2048 / channel 수: 96 / shared embedding, skip-z, orthogonal regularization을 모두 사용해 약 165000 iteration에서 중단한 모델)을 사용해 ImageNet으로 128x128, 256x256, 512x512 해상도로 평가했으며, 모델이 생성한 결과를 Figure 4를 통해 확인할 수 있습니다.

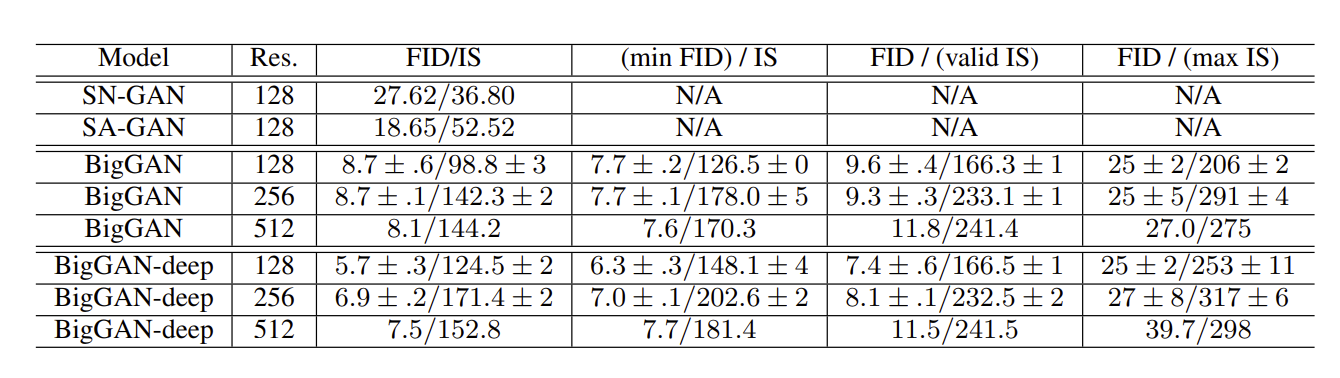
Table 2. 다양한 해상도에서의 모델 평가.
truncation이 없는 경우의 점수(3열), 가장 높은 FID 점수(4열), validation data의 IS 점수(5열), 가장 높은 IS 점수(6열)을 보고합니다.
표준 편차는 최소 3개의 random initialization에서 계산됩니다.

BigGAN은 다양성(variety)과 품질(fidelity) 간의 trade off에 따라 품질이 달라지기에, 품질을 극대화하기 위 각 모델이 달성하는 IS와 FID를 보고하며 모든 경우에서 BigGAN은 이전 state of the art의 IS와 FID 점수를 능가합니다.

논문은 BigGAN 외에도 residual block 구성을 사용하는 4배 더 깊은 모델인 BigGAN-deep을 제안합니다. Table 2에서 볼 수 있듯이 BigGAN-deep은 모든 해상도와 metric에서 BigGAN을 크게 능가하는 것을 볼 수 있는데 이는 논문의 연구 결과가 다른 구조로 확장되고 깊이가 증가하면 결과 품질이 향상된다는 것을 확인시켜줍니다. BigGAN과 BigGAN-deep의 해상도 별 구조들은 모두 논문의 Appendix B에 설명되어 있으니 구조를 보실 분들을 논문의 Appendix B를 참고해주세요!

Table 3. 256x256 해상도에서 JFT-300M으로 학습된 BigGAN의 결과
FID, IS 열은 JFT-300M으로 학습되었으며 noise 분포가 $z \sim \mathcal{N}(0, I)$인 Inception v2 판별 모델로 truncated되지 않은 상태에서 주어진 점수입니다.
(min FID) / IS와 FID / (max IS)열은 $\sigma = 0$에서 $\sigma = 2$ 범위에서 truncated된 noise 분포에서 보고된 가장 높은 FID와 IS를 보고합니다.
JFT-300M validation set의 이미지들에서는 IS가 50.88이고 FID가 1.94입니다.

저자들은 BigGAN이 ImageNet보다 훨씬 더 크고 복잡한 데이터에 효과적이라는 것을 확인하기 위해 JFT-300M의 부분 데이터에 대한 결과 또한 제시합니다. JFT-300M 데이터셋에는 18K개의 카테고리와 라벨이 지정된 300M 개의 이미지가 포함되어 있는데, 범주가 상당히 넓기 때문에 8.5K개의 의 일반적인 라벨을 가진 이미지만 유지해 데이터셋을 추출했으며 ImageNet보다 2배 큰 292M개의 이미지가 포함되어 있습니다.

이 데이터셋으로 학습한 Inception v2 판별 모델을 사용해 IS 및 FID를 계산했으며 결과는 Table 3에서 확인할 수 있습니다. 모든 모델은 batch size 2048로 학습됩니다. 또한 이런 규모의 데이터 셋인 경우, 모델의 channel을 확장함으로써 추가적인 개선 효과를 볼 수 있었다고 합니다.

Figure 8. $z$, $c$ 페어 사이의 보간

Figure 10. VGG-16-fc16 feature space에서 Nearest neightbor. 생성된 이미지는 가장 윗 행 왼쪽입니다.

또한 figure 8에서 이미지 간의 보간(interpolation)을, figure 10으로 결과 이미지의 nearest neighbor들을 제시합니다. BigGAN이 서로 다른 결과 사이를 설득력있게 보간하며 결과의 nearest neighbor들을 시각적으로 구별되는 것을 통해 모델이 단순히 학습 데이터를 기억(memorization)하지 않음을 보여줍니다.

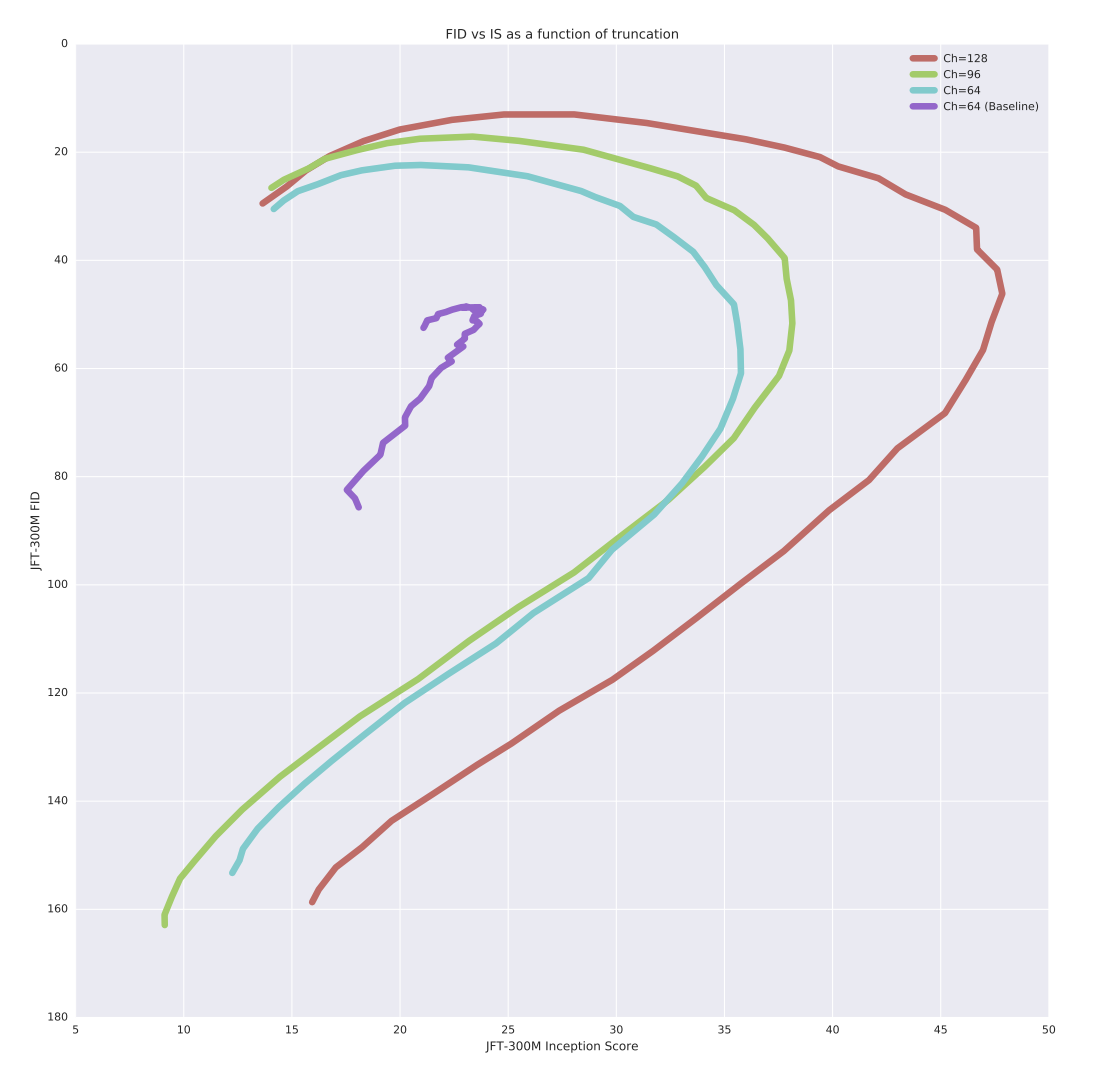
Figure 19. 256x256에서 JFT-300M IS vs FID. (2개 이미지 중 상단 이미지만 가져왔습니다)
truncation value는 $\sigma = 0$에서 $\sigma = 2$입니다.
각 곡선은 Table 3의 한 행에 해당합니다.
baseline으로 표시된 곡선만 orthogonal regularization과 여러 기술이 사용되지 않은 경우(Table 3, 1행)에 해당하며, 다른 곡선들은 같은 구조에서 다른 channel을 가진 Table 3의 2~4행에 해당합니다.

Figure 19에서 JFT-300M에서 학습된 모델에 대한 truncation plot을 제시합니다. $\sigma \approx 0$의 truncation limit에서 가장 높은 품질(fidelity)로 생성하는 경향이 있는 ImageNet과는 달리 JFT-300M에서는 truncation value $\sigma$가 0.5에서 1 사이일 때 최대화됩니다. 저자들은 JFT-300M 이미지 분포의 상대적 복잡성 때문에 원인 중 하나라 추측합니다.

흥미롭게도 무거운 regularization이 없다면 학습이 중단되는 경향이 있는 ImageNet 학습 모델과는 달리 JFT-300M에서 학습된 모델은 수십만 번의 iteration에 걸쳐 안정적으로 유지됩니다. 이는 ImageNet을 넘어 더 큰 데이터셋으로 이동할 경우 GAN 안정성 문제가 부분적을로 완화될 수 있음을 시사합니다.

결론으로 BigGAN은 품질(fidelity)와 다양성(variety) 모두에서 scaling up으로 큰 이득을 받는다는 것을 입증했으며 ImageNet GAN 모델 중 state of the art를 크게 향상시켰습니다. 또한 대규모 GAN에 대한 분석을 제시하고 weight의 singular value를 이용해 안정성을 부여하는 방법으로 안정성과 성능 사이의 상호작용에 대한 분석을 제시했습니다.

BIGGAN 논문 리뷰글의 끝입니다. 끝까지 봐주셔서 감사합니다:)

지금까지 논문 리뷰의 논문 중 appendix가 가장 긴 논문이였고 정말 다양하고 많은 실험들을 진행했다는 것을 알 수 있는 논문이었습니다. 글에는 적지 않았지만 논문의 Appendix H에서는 실험을 진행했지만 성능을 저하시키거나 영향을 미치지 못한 작업들이 나열되어 있으며 Appendix I에는 실험에 사용한 learning rate, R1 gradient penalty, Dropout rate, Adam $\beta_1$, Orthogonal Regularization penalty 수치들이 정리되어 있습니다. 직접 모델을 실험해 성능 또는 안정성을 개선하고자 하시는 분들에게는 많은 도움이 될 것 같으니 참고하시면 좋겠습니다.