CycleGAN(1) - 논문 리뷰
소개
이번 글은 CycleGAN 논문 리뷰입니다!![]()
![]()
![]()
기본적으로는 논문의 내용을 이해하기 위한 논문 번역을 적고 간단한 내용 요약과 추가 설명이 필요하다 생각되는 세션에는 [정리]로 설명을 적겠습니다.
Abstract
Image-to-Image 변환은 비전과 그래픽스 분야의 해결 과제 중 하나로 페어 이미지를 학습해 입력 이미지와 출력 이미지 사이의 매핑을 학습하는 것입니다. 하지만 많은 과제들에서 페어 이미지로 이루어진 학습 데이터를 사용할 수 없습니다. 우리는 페어 이미지의 데이터가 없는 경우 도메인 $X$에서 도메인 $Y$로 변환하는 방법을 학습하기 위한 접근 방식을 제안합니다. 우리의 목표는 $G : X \rightarrow Y$인 매핑 $G$를 학습하는 것으로 adversarial loss를 사용한 $G(X)$의 이미지 분포가 분포 $Y$와 구별할 수 없도록 하는 것입니다. 이 매핑은 제약이 매우 약하기 때문에 우리는 역 매핑인 $F : Y \rightarrow X$를 함께 사용하며 $F(G(X)) \approx X$(또는 그 반대)가 가능하도록 하는 cycle consistency loss를 소개합니다. style transfer, object transfiguration, season transfer, photo enhancement 등 학습 시 페어 데이터를 사용하지 않는 여러 과제에 대한 좋은 결과를 제시합니다. 몇몇 방법과 비교를 통해 우리의 접근 방식에 대한 우수성을 보여줍니다.
[정리]기존의 GAN 논문들과 마찬가지로 adversarial loss를 사용해 도메인 $X$의 데이터를 도메인 $Y$로 변화시키는 매핑 $G : X \rightarrow Y$를 사용합니다.
여기서 논문 제목의 근간이 된 cycle consistency loss를 추가로 사용합니다. 매핑 $G$의 역 매핑인 $F$는 도메인 $Y$를 도메인 $X$로 변화시키는 $F : Y \rightarrow X$의 역할을 합니다.
$F(G(X))$는 도메인 변화가 $X \rightarrow Y \rightarrow X$가 될 것이며 다시 도메인 $X$가 된 데이터가 원본 데이터와 비슷하기를 바라는 $F(G(X)) \approx X$를 cycle consistency loss로 사용합니다.
1. Introduction

Figure 1: 두 개의 이미지 데이터 $X$와 $Y$가 주어지면, 우리의 알고리즘은 이미지를 자동으로 원본에서 다른 것으로 “변환”하는 방법을 배웁니다. (왼쪽)Flickr의 모네 그림과 풍경 사진, (가운데)ImageNet의 얼룩말과 말, (오른쪽)Flickr의 Yosemite의 여름과 겨울 사진. (아래) : 유명한 예술가의 그림을 사용해 우리의 방법은 자연 사진을 각 스타일로 렌더링하는 방법을 배운다.
클로드 모네는 1873년 기분 좋은 봄에 Argenteuil 근처 Seine 강둑에 그의 이젤을 놓았을 때 무엇을 보았을까요?(Fgirue 1, top-left) 만약 컬러 사진이 발명되었다면, 상쾌한 푸른 하늘과 그것을 반사하는 유리 같은 강을 기록했을지도 모릅니다. 모네는 밝은 팔레트를 통해 그 장면에 대한 그의 느낌을 전달했습니다.
만약 모네가 시원한 여름 저녁에 Cassis의 작은 항구에서 일어나게 되었다면 어땠을까요?(Figure 1, bottom-left) 모네의 그림 갤러리를 잠시 확인해본다면 파스텔 색조, 갑작스러운 페인트 얼룩, 다소 잠잠한 역동성 등 그가 어떤 장면을 연출했을지 상상할 수 있습니다.
우리는 모네가 그린 장면에 대한 실제 사진과 바로 옆의 모네 그림이 나란히 있는 예시를 본 적이 없음에도 불구하고 이 모든 것을 상상할 수 있습니다. 우리에게는 모네 그림과 풍경 사진 데이터 셋에 대한 지식을 가지고 있습니다. 우리는 두 데이터 셋 사이의 스타일적인 차이에 대해 추론할 수 있기에 한 데이터 셋에서 다른 데이터셋으로 “변환”한다면 어떤 장면이 어떻게 보일지 상상할 수 있습니다.
본 논문에서는 위의 이론을 동일하게 학습할 수 있는 방법을 제시합니다. 즉, 한 이미지 데이터 셋의 특수성을 포착하고 이런 특성이 학습에 사용할 페어 데이터가 없는 경우에도 다른 이미지 데이터 셋으로 어떻게 변환될 수 있는지를 파악합니다.
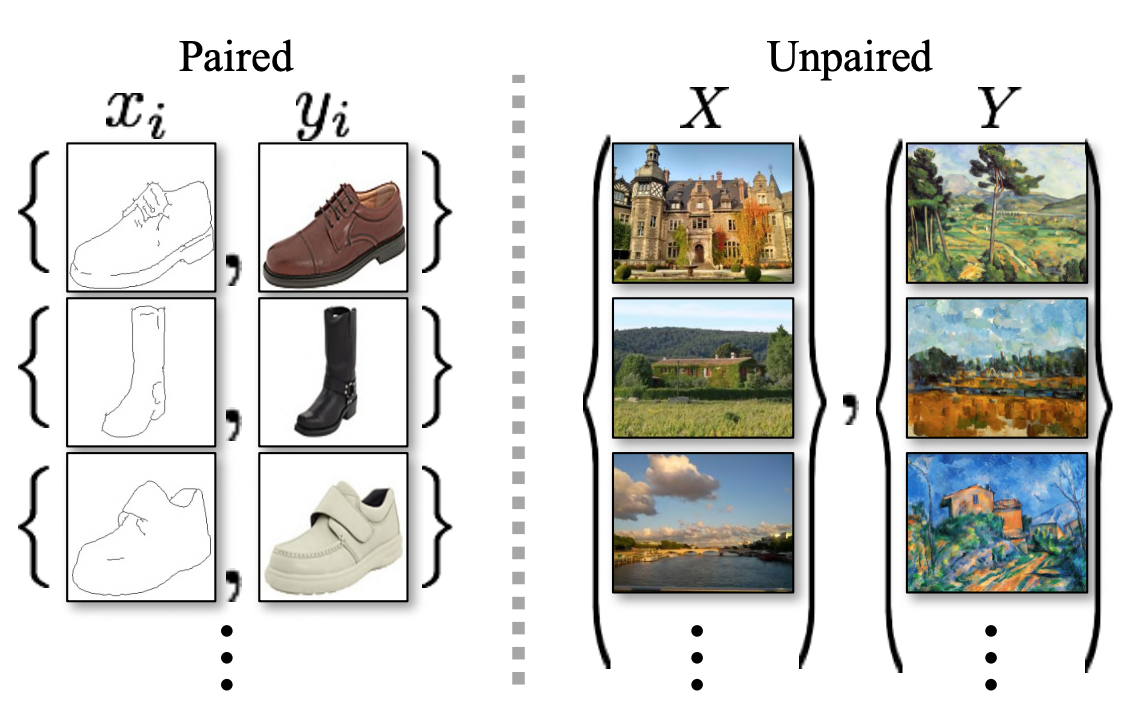
Figure 2: 페어를 이루는 학습 데이터(왼쪽)은 $x_i$와 $y_i$ 사이에 관계가 존재하는 pix2pix에서 사용하며 학습 예제는 $\lbrace x_i, y_i\rbrace ^N _{i=1}$로 이루어져 있습니다. 우리는 대신 $x_i$와 $y_i$ 간의 매칭되는 정보가 주어지지 않은 source 데이터 셋 $\lbrace x_i \rbrace ^N _{i=1} (x_i \in X)$와 target 데이터 셋 $\lbrace y_j \rbrace ^M _{j=1} (y_j \in Y)$로 이루어진 페어를 이루지 않는 학습 데이터(오른쪽)을 사용합니다.
이 문제는 주어진 장면의 한 표현인 $x$에서 다른 표현 $y$로 이미지를 변환하는 grayscale to color, image to semantic labels, edge-map to photograph와 같은 image-to-image 변환(pix2pix)으로 더 광범위하게 설명될 수 있습니다. 컴퓨터 비전, 이미지 처리, 컴퓨터 그래픽스에 대한 수년간의 연구는 지도학습 아래에서 페어 이미지 $\lbrace x_i, y_i \rbrace ^N _{i=1}$가 가능한 강력한 변환 시스템을 만들었습니다(Figure 2, left). 하지만 학습을 위한 페어 데이터를 얻는 것은 어렵고 비용이 많이 들 수 있습니다. 예를 들어, semantic segmentation과 같은 작업을 위한 데이터 셋을 오직 몇 개만 존재하며 상대적으로 수가 적습니다. 예술적 스타일 변환과 같은 그래픽 작업을 위한 입출력 페어 데이터를 얻는 것은 원하는 출력이 매우 복잡하며 일반적으로 저작권이 필요하기 때문에 훨씬 더 어려울 수 있습니다. 객체 변환(예시 : 얼룩말 $\leftrightarrow$ 말, Figure 1, top-middle)과 같은 많은 과제들의 경우 원하는 출력이 잘 정의되기 힘듭니다.
따라서 우리는 페어를 이루는 입력-출력 예제 없이 도메인 간 변환을 학습할 수 있는 알고리즘을 찾습니다(Figure 2, right). 우리는 도메인 사이에 어떤 기본 관계가 있다고 가정합니다. 예를 들어 도메인은 동일한 기본 장면의 두 가지 다른 렌더링이라고 가정하고 그 관계를 배우고자 합니다. 지도 학습에서 페어 데이터를 사용한 예시가 부족하지만 우리는 도메인 $X$의 이미지 셋과 다른 이미지 셋인 도메인 $Y$에 대한 데이터 셋이 제공되는 상태에서 지도학습을 이용할 수 있습니다. 우리는 $y$와 $\hat{y}$를 구별하도록 학습된 모델이 출력 $\hat{y} = G(x), x \in X$와 이미지 $y \in Y$를 구별할 수 없도록 매핑 $G : X \rightarrow Y$를 학습합니다. 이론적으로, 매핑 $G$는 분포 $p _{data}(y)$와 일치하는 $\hat{y}$에 대한 출력 분포를 유도할 수 있습니다. 따라서 최적의 $G$는 도메인 $X$를 $Y$와 동일하게 분포된 도메인 $\hat{Y}$로 변환합니다. 그러나 이러한 변환은 입력 $x$와 출력 $y$가 유의미하게 페어를 이룬다는 것을 보장하지 않으며 $\hat{y}$에 대해 동일한 분포를 유도하는 무한히 많은 매핑 $G$가 존재합니다. 더욱이 실제로 우리는 adversarial 목적 함수를 분리하여 최적화하는 것이 어렵다는 것을 알게 되었습니다. 일반적인 방법은 종종 모든 입력 이미지가 동일한 출력 이미지에 매핑되고 최적화가 이뤄지지 않는 mode collapse로 잘 알려진 문제를 초래합니다.
이러한 문제들은 우리의 목적 함수에 더 많은 구조를 추가할 것을 요구합니다. 따라서 우리는 변환 작업에 ‘주기적으로 일관되어야 한다(cycle consistent)’는 특성을 사용합니다. 예를 들어 영어에서 프랑스어로 문장을 번역한 다음, 프랑스어에서 영어로 다시 번역한다면 원래의 문장으로 돌아가야 합니다. 수학적으로, 만약 우리가 번역기 $G : X \rightarrow Y$와 또 다른 번역기 $F : Y \rightarrow X$를 가지고 있을 때 $G$와 $F$는 서로 반대의 기능을 수행해야 하며 두 매핑은 전단사 함수여야 합니다. 우리는 매핑 $G$와 $F$를 동시에 학습하고 ‘cycle consistency loss’를 추가해 $F(G(X)) \approx x$와 $G(F(y)) \approx y$가 가능하도록 합니다. 이 cycle consistency loss가 도메인 $X$와 $Y$의 adversarial loss와 결합하면 페어를 이루지 않은 image-to-image 변환에 대한 우리의 전체 목적 함수를 만들어 냅니다.
우리는 style transfer, object transfiguration, season transfer, photo enhancement를 포함한 응용 프로그램에 우리의 방법을 적용합니다. 또한 스타일과 컨텐츠의 factorization 또는 shared embedding functions에 의존하는 이전 접근 방식과 비교하여 우리의 방법이 이런 기준 모델을 능가한다는 것을 보여줍니다. 우리는 pytorch와 torch 구현을 모두 제공합니다. 우리의 웹사이트에서 더 많은 결과를 확인하세요.
[정리]페어 데이터는 데이터 셋의 수가 작기도 작고 만드는 데 비용이 많이 들며 출력에 대한 정의 또한 어렵습니다. 따라서 페어를 이루지 않는 데이터 셋을 사용하는 image-to-image 변환에 대한 알고리즘을 만들고자 합니다.
adversarial loss로 $p _{data}(y)$에 일치하는 $\hat{y}$에 대한 출력 분포를 유도할 수 있지만 입력 $x$와 출력 $y$가 유의미하게 페어를 이룬다는 것을 보장하지 않으며 mode collapse 문제가 발생할 수 있습니다. 이런 문제를 해결해하기 위해 $F(G(X)) \approx x$와 $G(F(y)) \approx y$가 가능하도록 cycle consistency loss를 추가합니다.
adversarial loss와 cycle consistency loss를 사용해 페어를 이루지 않은 데이터셋에서 image-to-image 변환이 가능하도록 합니다.
2. Related work
Generative Adversarial Networks(GANs)
GAN은 image generation, image editing, representation learning에서 인상적인 결과를 달성했습니다. 최근의 방법은 text2image, image inpainting, future prediction과 같은 조건부 이미지 생성 뿐만 아니라 비디오, 3D 데이터와 같은 다른 도메인에 대해서도 동일한 아이디어를 채택합니다. GANs의 성공 핵심은 생성된 이미지가 원칙적으로 실제 사진과 구별할 수 없도록 하는 adversarial loss에 대한 아이디어입니다. 이 loss는 많은 컴퓨터 그래픽이 최적화하려는 목표이기 때문에 특히 이미지 생성 작업에 강력하게 작용합니다. 우리는 변환된 이미지가 target 도메인과 구별할 수 없도록 매핑을 학습하기 위해 adversarial loss를 채택해 사용합니다.
Image-to-Image Translation
Image-to-Image 변환의 아이디어는 단일 입력-출력 페어 이미지에 non-parametric texture model을 사용한 Hertzmann의 Image Analogies 연구까지 거슬러 올라갑니다. 보다 최근의 접근 방식은 CNN을 사용하여 parametric translation function을 학습하기 위해 입력-출력 데이터 셋을 사용합니다. 우리의 접근 방식은 Isola의 ‘pix2pix’ 프레임 워크를 기반으로 하며 조건부 adversarial generation nerwork을 사용하여 입력 이미지에서 출력 이미지로의 매핑을 학습합니다. 비슷한 아이디어들이 sketch로부터 photographs를 생성하는 작업 또는 attribute와 semantic layout으로부터 photographs를 생성하는 작업과 같은 과제들에 적용되었습니다. 하지만 이전의 연구들과는 다르게 우리는 페어를 이루는 학습 데이터 없이 매핑하는 방법을 학습하고자 합니다.
Unpaired Image-to-Image Translation
페어를 이루지 않는 환경을 다루는 데 목표는 $X$와 $Y$라는 두 데이터 도메인을 연관시키는 것입니다. Rosales는 source image에서 계산된 patch 기반의 Markov random field와 여러 style image에서 얻은 likelihood term을 기반으로 하는 Bayesian framework를 제안합니다. 더 최근에는 CoGAN과 cross-modal scene network가 weight-sharing 전략을 사용해 도메인 간의 공통된 representation을 학습했습니다. 우리의 방법과 동시에 Liu는 variational autoencoders와 generative adversarial networks의 조합으로 프레임워크를 확장했습니다. 다른 계열에서 동시의 연구들은 입력과 출력이 ‘style’은 다를 수 있지만 특정 ‘content’ feature를 공유하도록 장려하는 연구들도 있었습니다. 또한 이러한 방법은 class label space, image pixel space, image feature space와 같이 사전 정의된 메트릭 공간에서 입력에 가까운 출력을 강제하는 추가적인 term과 함께 adversarial network를 사용합니다.
위의 접근 방식과 달리, 우리의 공식은 입력과 출력 사이의 작업 별 사전 정의된 유사성 함수에 의존하지 않으며 입력과 출력이 동일한 저차원 임베딩 공간에 있어야 한다고 가정하지도 않습니다. 이는 우리의 방법을 많은 비전 및 그래픽 작업을 위한 범용 솔루션으로 만듭니다. 우리는 Section 5.1.에서 이전의 몇가지 연구들과 현재 접근법을 직접 비교합니다.
Cycle Consistency
정형 데이터를 정규화하는 방법으로 transitivity를 사용하는 아이디어는 오랜 역사를 가지고 있습니다. visual tracking에서 단순한 forward-backward consistency를 시행하는 것은 수십 년 동안 표준적으로 사용한 방법이였습니다. 연어 영역에서 “back translation, reconciliation”을 통해 번역을 검증하고 개선하는 것은 기계뿐만 아니라 인간 번역가 또한 사용하는 기술힙니다. 보다 최근에는 motion, 3D shape matching, co-segmentation, dense semantic alignment, depth estimation의 구조에서 cycle consistency가 사용되었습니다.
Neural Style Transfer
Neural Style Transfer는 image-to-image 변환을 수행하는 또 다른 방법으로 사전 학습된 deep feature의 gram matrix와 일치하는 것을 기반으로 해 하나의 이미지의 콘텐츠를 다른 이미지의 스타일(일반적으로 그림)과 결합하여 새로운 이미지를 합성하는 방법입니다. 반면 우리의 주된 목적은 더 높은 수준의 외관 구조 간의 대응을 포착해 두 특정 이미지 간의 매핑이 아니라 두 이미지의 데이터 셋 간의 매핑을 배우는 것이빈다. 따라서 우리의 방법은 하나의 transfer 방법이 잘 수행되지 않는 작업들, object transfiguration 등의 다른 작업에 적용될 수 있습니다. 우리는 Section 5.2.에서 이 두가지 방법을 비교합니다.
논문의 목적인 image-to-image 변환 관련 연구로 gram matrix를 사용해 이미지를 합성하는 Neural Style Transfer와 조건부 adversarial 모델을 사용하는 연구들과 같은 선행 연구들이 있었습니다.
조건부 adversarial 모델 관련 연구들은 페어 데이터 셋을 사용했거나 페어를 이루지 않은 데이터 셋을 사용하더라도 연구 주제에 따라 연구 주제에 적합하도록 정의된 유사성 함수에 의존했습니다. Neural Style Transfer의 경우 이미지 2장으로 수행되어 데이터 셋 간의 매핑이 아니므로 수행되는 작업에 한계가 있습니다.
본 논문은 페어를 이루지 않는 학습 데이터 셋을 사용하며 연구 주제에 따라 유사성 함수를 따로 설정하지 않아도 되는 범용 솔루션을 제안합니다.
논문은 실제 데이터와 구별할 수 없도록 만드는 GANs의 adversarial loss와 Cycle consistency loss를 사용합니다.
3. Formulation
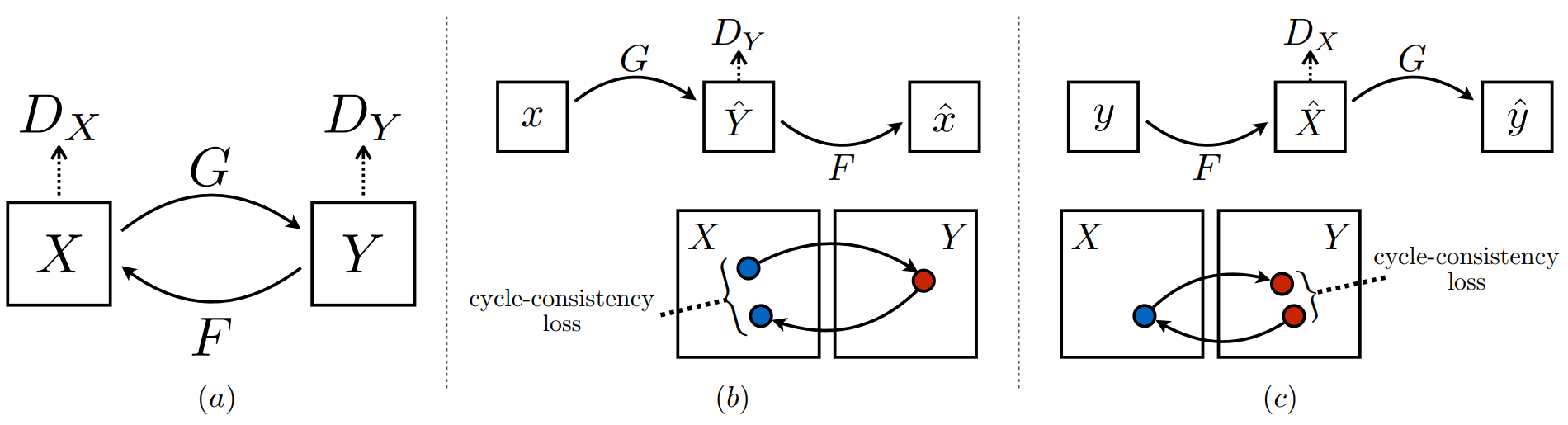
Figure 3: (a) 우리의 모델은 두 매핑 $G : X \rightarrow Y$와 $F : Y \rightarrow X$를 포함하며 adversarial discriminator인 $D_Y$와 $D_X$와 협동해 작동합니다. $D_Y$는 $G$가 모데인 $X$를 도메인 $Y$와 구별할 수 없는 결과로 변환할 수 있도록 장려하며 $D_X$와 $F$는 그 반대입니다. 매핑을 더욱 정교하게 하기 위해, 우리는 한 도메인에서 다른 도메인으로 변환하고 다시 되돌리면 우리가 시작한 곳에 도달해야 한다는 직관을 가진 두 가지 cycle consistency loss를 소개합니다. (b) forward cycle-consistency loss : $x \rightarrow G(X) \rightarrow F(G(x)) \approx x$, (c)backward cycle-consistency loss : $y \rightarrow F(y) \rightarrow G(F(y)) \approx y$
우리의 목표는 학습 데이터로 $x_i \in X$인 $\lbrace x_i \rbrace ^N _{i=1}$ 와 $y_j \in Y$인 $\lbrace y_j \rbrace ^M _{j=1}$를 가진 두 도메인 $X$와 $Y$ 사이를 매핑하는 함수를 학습하는 것입니다. 우리는 데이터 분포를 $x \sim p _{data}(x)$와 $y \sim p _{data}(y)$로 나타냅니다. Figure 3에서 표현된 것처럼 우리의 모델은 두 매핑 $G : X \rightarrow Y$와 $F : Y \rightarrow X$를 포함합니다. 추가로 우리는 2개의 adversarial discriminator인 $D_X$와 $D_Y$를 소개합니다. $D_X$는 이미지 $\lbrace x \rbrace$와 변환된 이미지 $\lbrace F(y) \rbrace$를 구별하는 것이 목적이고 같은 방법으로 $D_Y$는 이미지 $\lbrace y \rbrace$와 $\lbrace G(x) \rbrace$를 구별하는 것이 목적입니다. 우리의 목적은 생성된 이미지의 분포와 target 도메인의 데이터 분포를 매칭하기 위한 adversarial loss와 학습된 매핑 $G$와 $F$가 서로 부정하는 것을 막기 위한 cycle consistency loss, 총 두 종류의 term을 담고 있습니다.
[정리]도메인 $X$에서 도메인 $Y$로 변환하기 위한 매핑 $G$, 도메인 $Y$에서 도메인 $X$로 변환하기 위한 매핑 $F$를 adversarial loss를 이용해 학습합니다.
추가로 cycle consistency loss를 사용합니다. 두 매핑은 두 도메인 $X$와 $Y$ 간의 변환이므로 데이터 $x$에게 $G$와 $F$를 적용한 $F(G(x))$는 다시 도메인 $X$에 대한 데이터가 되기를 바라는 forward cycle consistency loss와 데이터 $y$에게 $F$와 $G$를 적용한 $G(F(x))$는 다시 도메인 $Y$에 대한 데이터가 되기를 바라는 backward cycle consistency loss를 cycle consistency loss로 적용해 학습합니다.
3.1. Adversarial Loss
우리는 adversarial loss을 두 매핑 함수 모두에 적용합니다. 우리는 매핑 함수 $G : X \rightarrow Y$와 판별 모델 $D_Y$를 목적 함수로 아래와 같이 표현합니다.
\[\mathcal{L} _{GAN}(G, D_Y, X, Y) = \mathbb{E} _{y \sim p _{data}(y)}[log D_Y(y)] + \mathbb{E} _{x \sim p _{data}(x)}[log(1-D_Y(G(x)))] \tag{1}\]$G$는 도메인 $Y$의 이미지들과 비슷해보이도록 이미지 $G(x)$를 생성하고 $D_Y$는 생성된 이미지 $G(x)$와 실제 이미지 $y$를 구별하는 것에 목적을 둡니다. $G$는 목적함수를 최소화하며 이에 대항하는 $D$는 목적함수를 최대화합니다. 즉, $\min_G \max _{D_Y} \mathcal{L} _{GAN} (G, D_Y, X, Y)$입니다. 우리는 매핑 함수 $F : Y \rightarrow X$ 뿐 만 아니라 이에 대한 판별 모델 $D_X$에 대해서도 유사한 adversarial loss를 도입합니다. 즉, $\min_F \max _{D_Y} \mathcal{L} _{GAN} (F, D_X, Y, X)$입니다.
[정리]GAN의 adversarial loss와 같은 식으로 $G$와 $D$의 기능 또한 같지만 매핑이 2가지라는 것에 차이가 있습니다.
생성 모델 $G$는 데이터 $x$를 도메인 $Y$의 분포와 비슷하도록 만들고 판별 모델 $D_Y$는 $G(x)$에 대해서 도메인 $Y$의 데이터인지 생성된 가짜 데이터인지 판별합니다. 역 매핑에 대해서도 마찬가지로 생성 모델 $F$는 데이터 $y$를 도메인 $X$의 분포와 비슷하도록 만들고 판별 모델 $D_X$는 $F(y)$가 도메인 $X$의 데이터인지 아닌지 판별합니다.
3.2. Cycle Consistency Loss
이론적으로 adversarial 학습은 각각 target 도메인 $Y$와 $X$로 동일하게 분포된 출력을 생성하는 매핑 $G$와 $F$를 학습할 수 있습니다. 그러나 복잡한 관계를 표현할 수 있는 정보를 담을 용량이 충분한 네트워크는 target 분포와 일치하는 출력 분포를 유도할 수 있지만 동일한 입력 이미지 셋을 target 도메인의 임의의 이미지에 매핑할 수 있습니다. 따라서 adversarial loss 만으로는 학습된 개별 함수가 개별 입력 $x_i$를 원하는 출력 $y_i$에 매핑할 수 있다고 보장할 수 없습니다. 가능한 매핑 함수의 공간을 줄이기 위해, 우리는 학습된 매핑 함수는 cycle-consistency 여야 한다고 주장합니다. Figure 3의 (b)에서 보여준 것처럼 도메인 $X$의 각각의 이미지 $x$에 대해서 이미지 변환 사이클은 원본 이미지 $x$로 다시 돌릴 수 있어야 합니다. 즉, $x \rightarrow G(x) \rightarrow F(G(X)) \approx x$입니다. 우리는 이것을 forward cycle consistency라 부릅니다. 유사하게 표현되는 Figure 3 (c)는 도메인 $Y$의 각각의 이미지 $y$에 대해서 $G$와 $F$는 backward cycle consistency : $y \rightarrow F(y) \rightarrow G(F(y)) \approx y$를 만족해야 합니다. 우리는 cycle consistency loss를 사용해 이를 장려합니다.
\[\mathcal{L} _{cyc} (G, F) = \mathbb{E} _{x \sim p _{data}(x)}[\| F(G(x))-x \|_1] + \mathbb{E} _{y \sim p _{data}(y)}[\| G(F(y))-y \|_1] \tag{2}\]선행 연구들에서 시도했던 것처럼 우리 또한 loss에 L1 norm을 $F(G(x))$와 $x$, $G(F(y))$와 $y$ 사이의 adversarial loss로 대체하려 시도했지만 향상된 성능을 관찰하진 못했습니다.

Figure 4: 다양한 실험에서의 입력 이미지 $x$, 출력 이미지 $G(x)$ 그리고 재구성된 이미지 $F(G(x))$. 위에서부터 아래까지 순서대로 photo $\leftrightarrow$ Cezanne, horses $\leftrightarrow$ zebras, winter Yosemite $\leftrightarrow$ summer Yosemite, aerial photos $\leftrightarrow$ google maps
cycle consistency loss로 인한 결과를 Figure 4에서 확인할 수 있습니다. 재구성된 $F(G(x))$는 입력 이미지 $x$와 유사하게 매칭됩니다.
[정리]생성 모델 $G$가 $\lbrace x_i \rbrace$를 도메인 $Y$의 분포와 일치하도록 변환한 $G(x)$가 원하는 출력인 $\lbrace y_i \rbrace$에 일치하지 않을 수 있습니다. 대표적인 예시로는 생성 모델이 어떤 입력에서도 같은 출력을 내놓는 Mode Collapse 가 있습니다. 이 문제를 해결하기 위해 생성한 $G(x)$를 생성 모델 $F$에 입력해 다시 도메인 $X$로 변환한 $F(G(x))$와 원본 데이터인 $x$와 L1 loss를 사용해 최대한 일치하도록 만드는 cycle consistency loss를 도입합니다.
매핑 함수가 2개이니 cycle consistency loss도 2개로 구별할 수 있습니다.
forward cycle consistency는 source 데이터 $x$와 $F(G(x))$와의 L1 loss를 계산하며 backward cycle consistency는 target 데이터 $y$와 $F(G(y))$와의 L1 loss를 계산합니다.
3.3. Full Objective
우리의 목적 함수는 아래와 같습니다.
\[\mathcal{L}(G, F, D_X, D_Y) = \mathcal{L} _{GAN} (G, D_Y, X, Y) + \mathcal{L} _{GAN} (F, D_X, Y, X) + \lambda \mathcal{L} _{cyc}(G, F) \tag{3}\]여기서 $\lambda$는 두 목적의 상대적 중요성을 제어합니다. 우리는 아래를 수식을 해결하는 것을 목표로 합니다.
우리의 모델은 “autoencoders“를 학습하는 것으로 볼 수 있습니다. 우리는 하나의 autoencoder $F \circ G : X \rightarrow X$와 다른 antoencoder $G \circ F : Y \rightarrow Y$를 함께 학습합니다. 그러나 이런 autoencoder들은 각각 이미지를 다른 도메인으로 변환하는 중간 표현을 통해 이미지를 자신에게 매핑하는 특별한 내부 구조를 가지고 있습니다. 이러한 설정은 임의의 target 분포와 일치하도록 autoencoder의 bottleneck 레이어를 학습하기 위해 adversarial loss를 사용하는 “adversarial autoencoder“의 특별한 경우로 볼 수 있습니다. 이 경우 $X \rightarrow X$를 수행하는 autoencoder의 target 분포는 도메인 $Y$의 분포입니다.
Section 5.1.4 에서는 adversarial loss $\mathcal{L} _{GAN}$을 단독으로 사용한 것과 cycle consistency loss $\mathcal{L} _{cyc}$를 단독으로 사용한 것을 포함해 목적 함수의 일부와 전체 목적 함수를 비교하고, 두 목적이 고품질 결과에 도달하는 데 중요한 역할을 한다는 것을 경험적으로 보여줍니다. 또한 우리는 한 방향의 cycle loss만 가지고 우리의 방법을 평가하고 한 방향의 cycle loss로는 제한되지 않는 문제에 대한 학습을 정규화하기에 충분하지 않다는 것을 보여줍니다.
[정리]최종 목적 함수는 Equation 3으로 위에서 설명된 GAN loss(adversarial loss)와 cyc loss(cycle consistency loss)를 사용합니다.
autoencoder는 input $x$ $\rightarrow$ encoder $\rightarrow$ $z$ $\rightarrow$ decoder $\rightarrow$ output $x$의 구조를 가집니다. 여기서 encoder를 $G$, decoder를 $F$로 이해한다면 입력 값이 $G$(encoder)를 통해 다른 값으로 변하고 다시 $F$(decoder)를 통해 원래의 값으로 돌아오는 모양이 되며 CycleGAN의 모델과 같은 모양이라 볼 수 있게 됩니다.
중간 표현인 $z$가 bottleneck 레이어를 통해 나오게 되는데 이 $z$가 도메인 $Y$, input $x$와 output $x$를 도메인 $X$로 본다면 autoencoder로 도메인 변화가 $X \rightarrow Y \rightarrow X$가 되므로 논문과 일치한다 할 수 있습니다.
adversarial loss만 사용한 경우, cycle consistency loss만 사용한 경우, adversarial + forward cycle consistency loss를 사용한 경우, adversarial + backward cycle consistency loss를 사용한 경우, adversarial + cycle consistency loss를 사용한 경우를 실험한 결과를 Section 5.1.4에서 확인할 수 있습니다.
4. Implementation
Network Architecture
우리는 neural style transfer와 super resolution에 대해 인상적인 결과를 보여준 Johnson의 생성 네트워크를 사용합니다. 이 네트워크는 3개의 convolution, 여러 residual blocks, $\frac{1}{2}$의 stride를 가진 2개의 fractionally-strided convolution 그리고 feature map을 RGB에 매핑하는 convolution 하나를 포함합니다. 128x128 이미지에는 6개의 block을 사용하고 256x256 이상의 고해상도 학습 이미지에는 9개의 block을 사용합니다. Johnson과 비슷하게 우리는 instance normalization을 사용합니다. 판별 모델 네트워크의 경우 70x70 PatchGAN를 사용하며 70x70 부분 이미지 패치가 실제인지 가짜인지를 분류합니다. 이런 패치 수준 판별 모델 아키텍처를 전체 이미지 판별 모델보다 매개 변수가 적으며, fully convolutional fashion 방식으로 임의의 크기의 이미지에서 작용할 수 있습니다.
Training details
우리는 모델 학습 절차를 안정화하기 위해 최근 연구의 2가지 기술을 적용합니다. 첫번째로 $\mathcal{L} _{GAN}$ (Equation 1)의 경우 negative log likelihood 목적을 least-squares loss로 대체합니다. 이 손실은 훈련 중에 더 안정적이고 더 높은 품질의 결과를 생성합니다. 특히 GAN loss $\mathcal{L} _{GAN}(G, D, X, Y)$를 위해 우리는 $\mathbb{E} _{x \sim p _{data}(x)}[(D(G(x)) - 1) ^2]$를 최소화하도록 $G$를 학습하고 $\mathbb{E} _{y \sim p _{data}(y)}[(D(y) - 1) ^2] + \mathbb{E} _{x \sim p _{data}(x)}[D(G(x)) ^2]$를 최소화하기 위해 $D$를 학습합니다.
두번째로 model oscillation를 줄이기 위해, 우리는 Shrivastava의 전략을 따르고 마지막 생성 모델이 생성한 하나의 이미지가 아닌 생성된 이미지 히스토리를 사용해 판별 모델을 업데이트합니다. 우리는 이전에 생성된 50개의 이미지를 저장하는 이미지 버퍼를 가지고 있습니다.
모든 실험에서, 우리는 Equation 3의 $\lambda = 10$으로 설정했다. 우리는 배치 크기가 1인 Adam solver을 사용합니다. 모든 네트워크는 0.0002의 학습률을 가지고 학습되었습니다. 우리는 처음 100 epoch 동안 학습률을 유지하고 다음 100 epoch 동안 학습률을 0으로 감소시킵니다
[정리]생성 모델은 Perceptual Losses for Real-Time Style Transfer and Super-Resolution의 생성 네트워크를 사용하며 판별 모델은 pix2pix에서도 사용한 PatchGAN을 사용합니다.
기존의 GAN에서는 cross entropy를 사용하는 게 일반적이였지만 본 논문에서는 LSGAN의 least square loss를 사용하며 이미지 버퍼를 사용해 판별 모델을 업데이트하는 것과 learning rate scheduler를 사용하는 것이 특징입니다.
5. Results
우리는 input-output 페어를 이루고 있는 데이터 셋에 페어를 이루지 않은 image-to-image 변환을 시도하는 모델에 대해서 최근의 연구들과 우리의 접근 방식을 비교합니다. 이후 adversarial loss와 cycle consistency loss의 중요성을 연구하고 전체 loss에 대해 변형된 방법들과 비교합니다. 미자믹으로, 우리는 페어를 이룬 데이터가 존재하지 않는 광범위한 응용 프로그램에서 알고리즘의 일반성을 입증합니다. 우리는 우리의 방법을 간략하게 CycleGAN이라 부릅니다. PyTorch 및 Torch 코드, 모델, 전체 결과는 우리의 웹사이트에서 확인할 수 있습니다.
5.1. Evaluation
pix2pix와 동일한 데이터 셋 및 메트릭을 사용해 우리의 방법을 질적으로나 양적으로 여러 기준 모델들과 비교합니다. 작업에는 Cityscapes 데이터 셋에서의 semantic labels $\leftrightarrow$ photo와 Google Maps에서 스크랩한 데이터의 map $\leftrightarrow$ aerial photo가 포함됩니다. 또한 우리는 전체 loss 함수에 대한 ablation study를 수행합니다.
ablation study
모델이나 알고리즘를 이루고 있는 부분들의 영향을 테스트하는 방법입니다. 예시로 모델을 a, b, c로 구분할 수 있다면 {a, b, c, ab, bc, abc}를 테스트해 모델의 특정 부분의 성능과 영향력을 평가하는 실험을 의미합니다.참고
- Fintecuriosity님의 [데이터 사이언스]"Ablation study"란 무엇인가?
5.1.1 Evaluation Metrics
AMT perceptual studies
map $\leftrightarrow$ aerial photo 연구에서 우리는 Amazon Mechanical Turk(AMT)에 대한 “real vs fake” 지각 연구를 통해 우리 결과에 대한 현실성을 평가합니다. 우리는 pix2pix와 동일한 지각 연구 프로토콜을 따릅니다. 단, 테스트한 알고리즘 당 25명의 참가자로부터만 데이터를 수집합니다. 참가자들에게는 실제 사진이나 지도, 가짜 이미지(알고리즘이나 기준 모델에 의해 생성된 이미지) 등 일련의 이미지를 보여주고 실제라고 생각하는 생각하는 이미지를 클릭하도록 요청되었습니다. 각 세션의 처음 10번의 시행은 연습으로 참가자의 응답에 대한 정답 피드백이 주어집니다. 이후 나머지 40번의 시행에서는 응답에 대한 피드백이 주어지지 않으며 응답이 참가자들을 속인 비율을 계산하는 데 사용됩니다. 참가자는 하나의 알고리즘만 테스트할 수 있습니다. 우리가 보고하는 수치는 우리의 ground truth 이미지가 pix2pix와는 다르게 처리되었고 우리가 테스트한 참가자들이 pix2pix에서 테스트한 것과 다르게 분포할 수 있기 때문에 pix2pix의 숫자와 직접 비교할 수는 없습니다. 따라서 우리의 수치는 pix2pix에 대한 것이 아니라 동일 조건에서 실행된 기준 모델들과 우리의 방법을 비교하는 데만 사용되어야 합니다.
FCN score
지각 연구가 그래픽의 현실성을 평가하는 기준일 수 있지만, 우리는 사람이 참가하는 실험이 필요하지 않는 자동 정량적 측정을 추구합니다. 이를 위해 pix2pix의 “FCN score”를 채택하고, 이를 사용하여 Cityscapes label $\rightarrow$ photo 실험을 평가합니다. FCN 방법은 사용 가능한 semantic segmentation 알고리즘에 따라 생성된 사진이 기존 모델에 의해 얼마나 해석 가능한지 평가합니다. FCN은 생성된 사진에 대한 label map을 예측해 아래에 설명된 standard semantic segmentation 방법을 사용해 입력된 ground truth label과 비교합니다. 직관적으로 “도로 위의 자동차” label map에서 사진을 생성했을 때 생성된 사진에 FCN(semantic segmentation)이 “도로 위의 자동차”를 감지한다면 성공한 것이 됩니다.
Semantic segmentation metrics
photo $\rightarrow$ label의 성능을 평가하기 위해, 우리는 데이터 셋 당 정확도, 클래스 당 정확도, 평균 class intersection-Over-Union(class IOU)을 포함한 Cityscapes 벤치마크의 표준 방법을 사용합니다.
pix2pix에서 소개했던 AMT과 FCN score와 같은 방법을 사용합니다.
AMT는 사람이 주어진 이미지를 보고 진짜인지 가짜인지 판단하는 실험으로 생성된 이미지가 얼마나 많은 사람들에게 진짜 이미지처럼 보여 사람들을 속일 수 있는지에 대한 퍼센트를 분석합니다. 처음 10장의 이미지에 대해서는 실험자들에게 해당 이미지가 진짜 이미지인지 생성된 이미지인지에 대한 피드백을 주며 이후 40장에 대한 실험자들의 답변이 실험 결과로 분석됩니다.
FCN은 기존의 semantic segmentation 모델을 사용해 생성 이미지 내의 object들을 얼마나 정확하게 클래스 별로 픽셀에 나타내는 지를 실험합니다. 생성된 이미지과 현실의 이미지와 유사할 수록 segmentation 모델 또한 더 정확하게 이미지 내의 object 들을 segmentation 할 수 있을 것이라는 아이디어로 segmentation 결과의 class 별 정확도, IOU 등을 분석합니다
5.1.2 Baselines
CoGAN
이 방법은 shared latent representation을 위해 처음 몇 개의 레이어에 묶인 가중치를 사용해 도메인 $X$에 대해 하나의 GAN 생성모델과 도메인 $Y$에 대해 하나의 GAN 생성 모델을 학습합니다. $X$에서 $Y$로의 변환은 이미지 $X$를 생성하는 latent representation을 찾은 다음 이 latent representation을 스타일 $Y$로 렌더링해 달성할 수 있습니다.
SimGAN
우리의 방법과 비슷하게 SimGAN은 $X$에서 $Y$로의 변환을 학습하기 위해 adversarial loss를 사용합니다. 정규화 term $|x-G(x)|_1$은 픽셀 수준에서 큰 변화를 일으키는 데 불이익을 주는 데 사용됩니다.
Feature loss + GAN
우리는 L1 loss가 RGB 픽셀 값이 아닌 사전 학습된 네트워크(VGG-16 relu4_2)를 사용해 deep image feature에 대해 계산되는 SimGAN의 변형을 테스트합니다. 이와 같이 deep feature 공간에서의 거리 계산은 때때로 “perceptial loss”를 사용하는 것으로 언급되기도 합니다.
BiGAN / ALI
조건이 주어지지 않은 GANs는 랜덤 노이즈 $z$를 이미지 $x$에 매핑하는 생성 모델 $G : Z \rightarrow X$를 학습합니다. BiGAN 및 ALI은 역 매핑 함수 $F : X \rightarrow Z$도 학습할 것을 제안합니다. 기존에는 잠재 벡터 $z$를 이미지 $x$에 매핑하기 위해 설계되었지만 우리는 source 이미지 $x$를 target 이미지 $y$에 매핑하기 위해 동일한 목적함수를 사용했습니다.
pix2pix
우리는 또한 페어를 이룬 데이터에 대해 학습된 pix2pix와 비교하여 페어 데이터를 사용하지 않고 이 “upper bound”에 얼마나 근접할 수 있는지 확인했습니다. 공정한 비교를 위해 우리는 CoGAN를 제외한 모든 베이스라인들은 같은 아키텍처와 디테일로 구현했습니다. CoGAN은 image-to-image 네트워크과 호환되지 않는 shared latent representation에서 이미지를 생성하는 생성 모델을 기반으로 하기 때문에 같은 구조로 구현하지 못했으나 대신 CoGAN의 공개된 구현을 사용해 비교에 사용했습니다.
기준이 되는 모델들에 대한 간략한 설명들입니다.
여기서 pix2pix가 페어 데이터를 사용하는 모델로 상한선(upper-bound)의 역할을 합니다. 페어 데이터를 사용하지 않고 페어 데이터를 사용하는 pix2pix를 얼마만큼 따라잡을 수 있는 지가 주요하게 봐야할 부분 중 하나입니다.
5.1.3 Comparison against Baselines

Figure 5: Cityscapes 이미지들로 학습된 labels $\leftrightarrow$ photos을 위한 여러 방법들. 왼쪽부터 오른쪽까지 순서대로 : 입력 이미지, BiGAN/ALI, CoGAN, feature loss + GAN, SimGAN, CycleGAN(ours), 페어를 이룬 데이터로 학습된 pix2pix, ground truth 이미지

Figure 6: Google Maps의 aerial photos $\leftrightarrow$ maps에 대한 여러 방법들. 왼쪽부터 오른쪽까지 순서대로 : BiGAN/ALI, CoGAN, feature loss + GAN, SimGAN, CycleGAN(ours), 페어를 이룬 데이터로 학습된 pix2pix, ground truth 이미지
Figure 5와 Figure 6에서 볼 수 있듯이, 우리는 어떤 기준 모델에서도 설득력 있는 결과를 얻을 수 없었습니다. 반면, 우리의 방법은 종종 완전히 지도학습된 pix2pix와 유사한 품질의 변환을 생성할 수 있습니다.

Table 1: 256x256 해상도의 maps $\leftrightarrow$ aerial photo에 대한 AMT “real vs fake” 실험
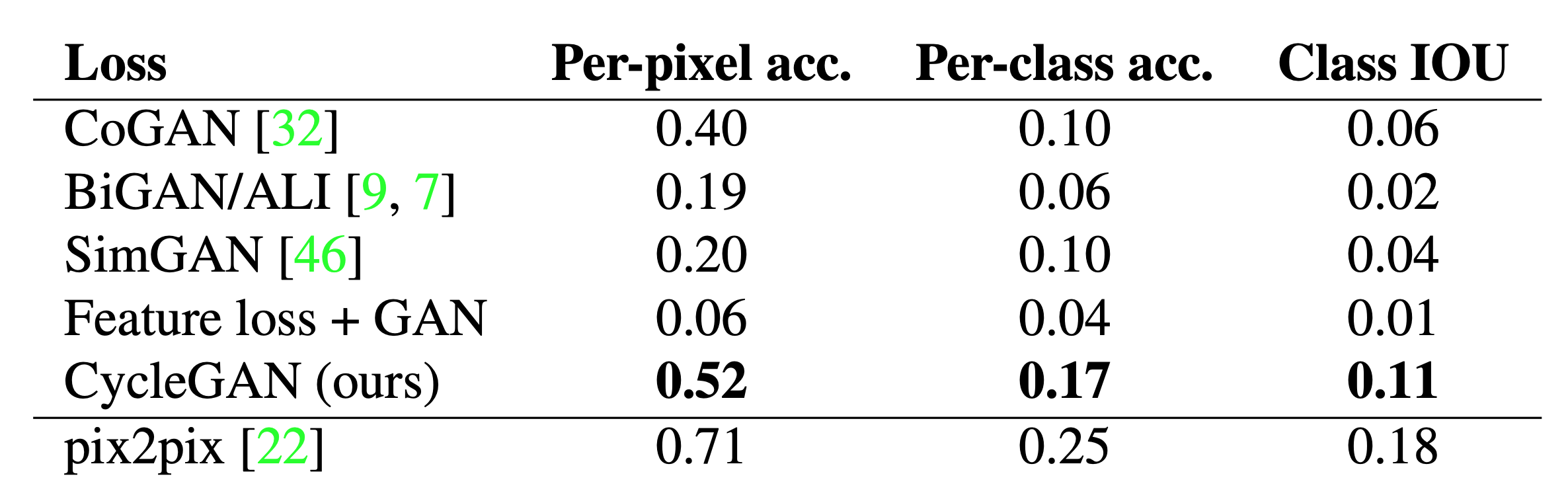
Table 2: Cityscapes의 labels $\rightarrow$ photo에 대한 FCN score
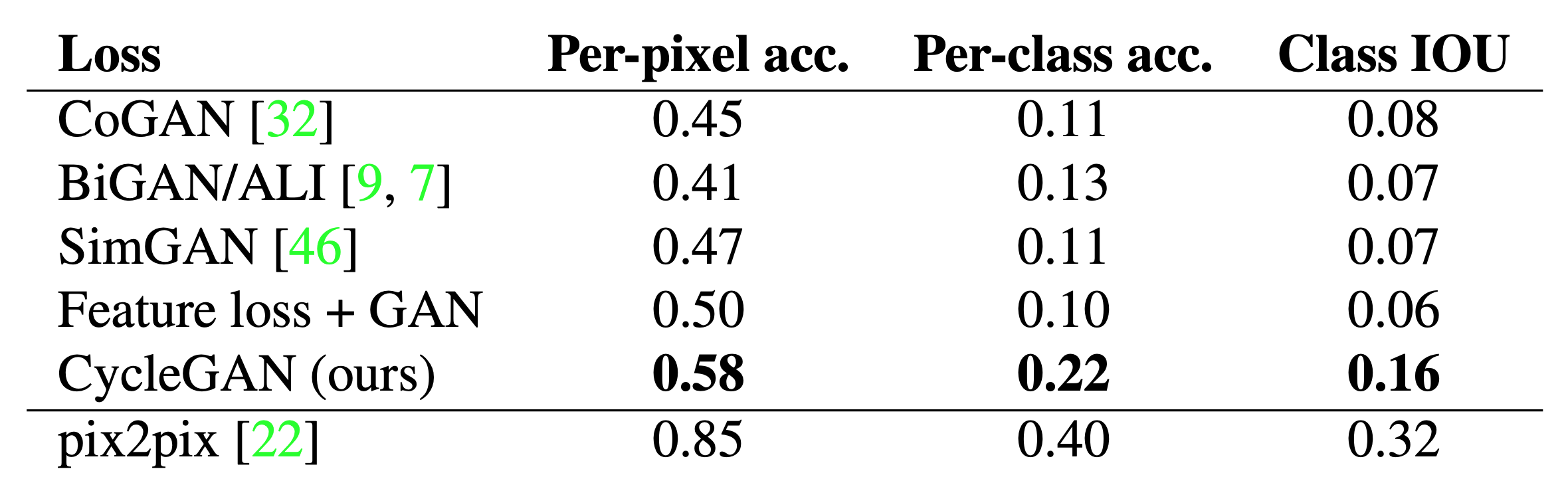
Table 3: Cityscapes의 photo $\rightarrow$ labels 에 판별 성능
Table 1은 AMT 인식 실험과 관련된 성능을 보여줍니다. 여기서, 우리는 우리의 방법이 256x256 해상도에서 maps → aerial photos 과 aerial photos → maps 모두 참가자들의 약 4분의 1 정도를 실험에서 속일 수 있다는 것을 알 수 있었습니다. 비교 대상인 기준 모델들은 모두 참가자들을 거의 속이지 못했습니다. 우리는 또한 CycleGAN과 pix2pix를 512x512 해상도로 학습하고 비교할 만한 성능을 관찰한 결과 maps → aerial photos에서 CycleGAN은 37.5% $\pm$ 3.6%의 결과가 나왔으며 pix2pix는 33.9% $\pm$ 3.1%의 결과가 나왔습니다. 반대로 aerial photos → maps 실험에서는 CycleGAN이 16.5% $\pm$ 4.1 %의 결과가 나왔고 pix2pix는 8.5% $\pm$ 2.6%의 결과가 나왔습니다.
Table 2는 Cityscapes에 대해 labels → photo의 성능을 평가하고 Table 3은 반대 매핑(photos → labels)을 평가합니다. 두 경우 모두, 우리의 방법은 다시 모든 기준 모델들을 능가합니다.
[정리]Cityscapes 데이터 셋에서 실험한 labels $\leftrightarrow$ photos와 Google Maps 데이터 셋에서 실험한 aerial photos $\leftrightarrow$ maps 에서 모두 다른 기준 모델들을 크게 뛰어넘는 성능을 보여주었습니다. 하지만 두 데이터셋은 페어 데이터 셋이며 페어 데이터로 학습한 pix2pix를 따라잡지는 못함을 보여줍니다.
5.1.4 Analysis of the loss function
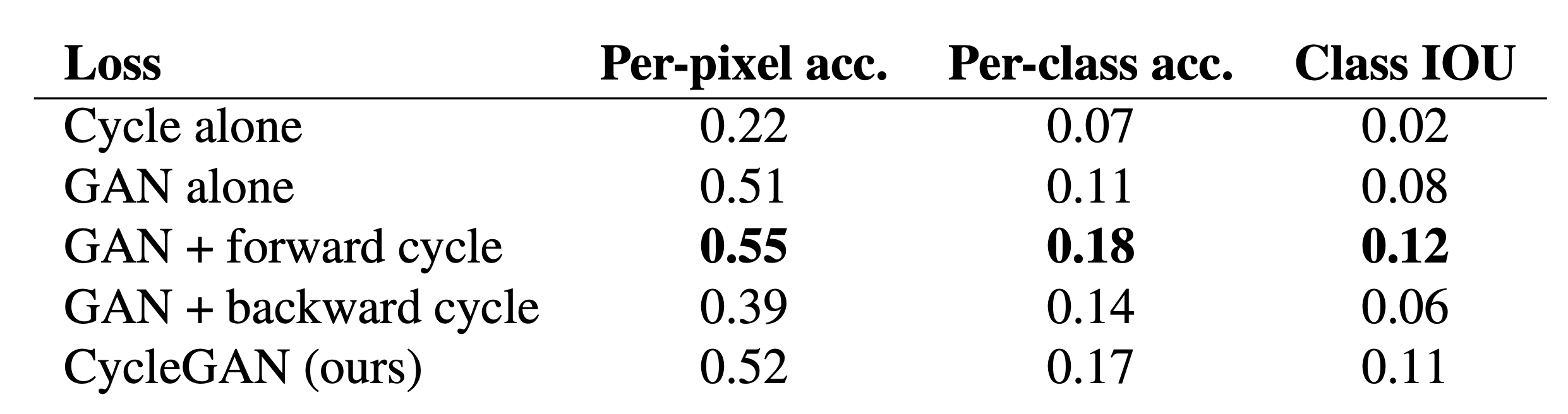
Table 4: Ablation study : Cityscapes labels $\rightarrow$ photo에서 평가된 우리의 방법의 다양한 변형에 대한 FCN-scores
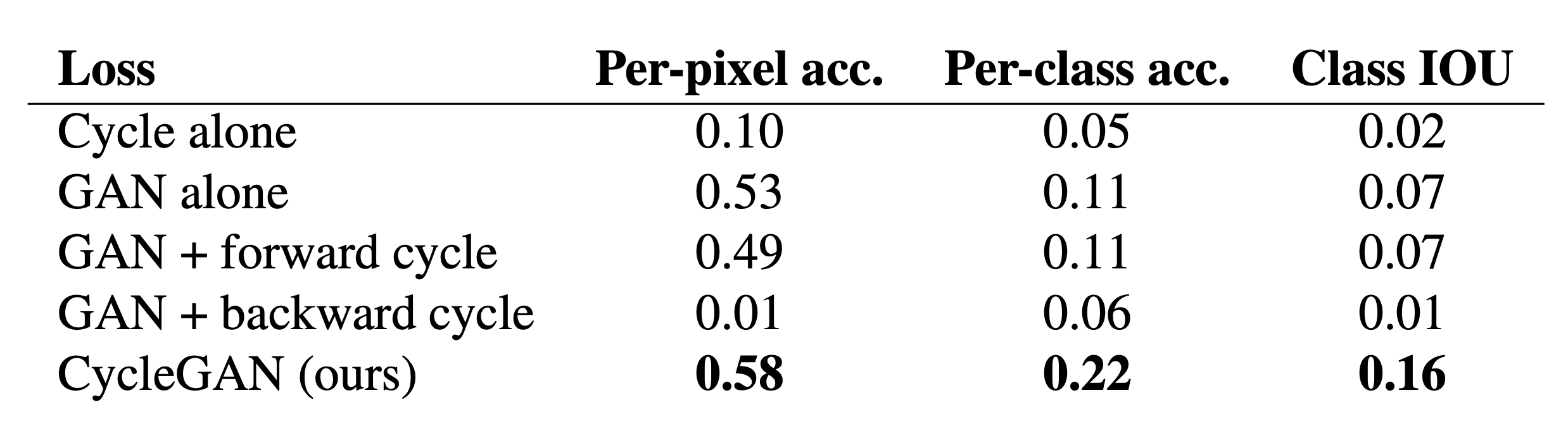
Table 5: Ablation study : Cityscapes의 photo $\rightarrow$ labels 에 대해 평가된 다양한 loss 들의 판별 성능

Figure 7: Cityscapes에서 학습된 label $\leftrightarrow$ photos 매핑을 위한 우리의 방법의 다양한 변형. 왼쪽에서 오른쪽으로 순서대로 : input, cycle-consistency loss alone, adversarial loss alone, GAN + forward cycle-consistency loss $(F(G(x)) \approx x)$, GAN + backward cycle-consistency loss $(G(F(x)) \approx y)$, CycleGAN(우리의 full method), ground truth. Cycle alone과 GAN + Backward 모두 target 도메인과 유사한 이미지를 생성하지 못합니다. GAN 단독 및 GAN + forward는 mode collapse로 인해 입력 사진과 상관 없이 동일한 label map을 생성합니다.
Table 4와 Table 5에서, 우리는 우리의 최종 loss와 ablations들을 비교합니다. GAN loss를 제거하는 것은 cycle-consistency loss를 제거하는 것과 마찬가지로 결과를 상당히 저하시킵니다. 따라서 우리는 두 term 모두 결과에 중요하다고 결론짓습니다. 우리는 또한 우리의 방법을 한 방향으로의 cycle loss로 GAN + forward cycle loss인 $\mathbb{E} _{x \sim p _{data}(x)}[| F(G(x))-x|_1]$ 와 GAN + backward cycle loss인 $\mathbb{E} _{y \sim p _{data}(y)}[| G(F(y))-y|_1]$(Equation 2)를 평가했으며 특히 제거된 매핑의 방향에서 대한 학습 불안정성을 유발하고 mode collapse를 유방하는 경우가 많다는 것을 발견했습니다. Figure 7은 몇 가지 질적인 예시를 보여줍니다.
[정리]loss function은 크게 GAN loss와 cycle consistency loss로 나눠져 있으며 Ablation study 결과 두 loss 모두 사용했을 때 가장 성능이 높았음을 확인할 수 있습니다. 또한 cycle consistency loss는 forward와 backward로 나눠지는데 단일방향만 사용한다면 mode collapse가 발생하는 등 학습이 불안정해졌으며 mode collapse가 발생했음을 Figure 7에서 확인할 수 있었습니다.
5.1.5 Image reconstruction quality

Figure 4: 다양한 실험에서의 입력 이미지 $x$, 출력 이미지 $G(x)$ 그리고 재구성된 이미지 $F(G(x))$. 위에서부터 아래까지 순서대로 photo $\leftrightarrow$ Cezanne, horses $\leftrightarrow$ zebras, winter Yosemite $\leftrightarrow$ summer Yosemite, aerial photos $\leftrightarrow$ google maps
Figure 4에서는 재구성된 이미지 $F(G(x))$의 몇 가지 무작위 예제들을 보여줍니다. 우리는 재구성된 이미지가 종종 학습과 테스트 모두에서 원래 입력 $x$에 가깝다는 것을 관찰했으며 심지어 maps ↔ aerial photo와 같이 훨씬 더 다양한 정보를 나타내는 도메인인 경우에도 성립했습니다.
5.1.6 Additional results on paired datasets

Figure 8: labels $\leftrightarrow$ photos과 edges $\leftrightarrow$ shoes 와 같은 pix2pix에서 사용된 페어 데이터셋에 대한 CycleGAN의 결과 예시
Figure 8은 CMP Facade Database의 labels $\leftrightarrow$ photos와 UT Zappos50K dataset의 edges $\leftrightarrow$ shoes와 같은 “pix2pix”에서 사용된 페어 데이터셋에 대한 몇몇 결과 계시를 보여줍니다. 우리의 결과 이미지 품질은 완전히 지도된 pix2pix에 의해 생성된 것에 가까우며 우리의 방법은 페어를 이룬 지도학습 없이 매핑을 학습합니다.
5.2 Applications
우리는 페어를 이룬 학습 데이터가 존재하지 않는 여러 응용 프로그램에서 우리의 방법을 시연합니다. 우리는 학습 데이터에 대한 변환이 종종 테스트 데이터에 대한 변환보다 더 매력적이라는 것을 관찰했으며, 학습 및 테스트 데이터에 대한 모든 응용 프로그램의 전체 결과는 프로젝트 웹 사이트에서 볼 수 있습니다.
Collection style transfer

Figure 10: style transfer 1 : 입력 이미지는 Monet, Van Gogh, Cezanne, Ukiyo-e의 예술적 스타일로 입력 이미지를 변환합니다.

Figure 11: style transfer 2 : 입력 이미지는 Monet, Van Gogh, Cezanne, Ukiyo-e의 예술적 스타일로 입력 이미지를 변환합니다.
우리는 Flickr와 WikiArt에서 다운로드한 풍경 사진에 대해 모델을 학습시킵니다. “neural style transfer”에 대한 최근의 연구와 달리, 우리의 방법은 선택된 단일 예술 작품의 스타일을 이전하는 대신 전체 예술 작품의 스타일을 모방하는 방법을 배웁니다. 따라서, 우리는 단지 별이 빛나는 밤의 스타일이 아닌, Van Gogh의 스타일로 사진을 생성하는 것을 배울 수 있습니다. 각 아티스트/스타일에 대한 데이터 셋의 크기는 Cezanne, Monet, Van Gogh, Ukiyo-e의 경우 526, 1073, 400, 562이었습니다.
Object transfiguration
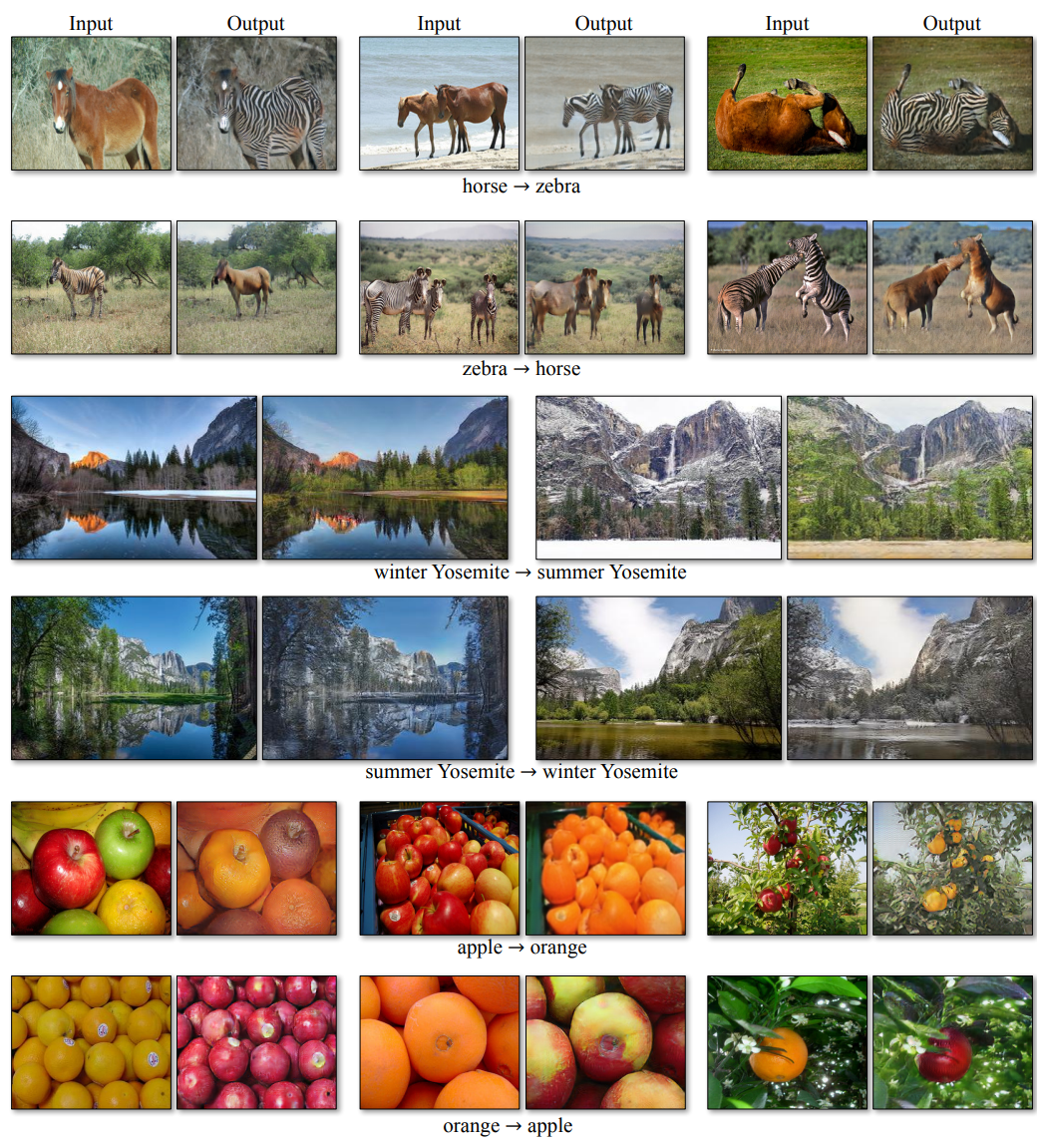
Figure 13: 우리의 방법을 몇 가지 변환 문제에 적용했습니다. 이 이미지들은 비교적 성공적인 결과로 선택되었으며 보다 포괄적이고 무작위적인 결과는 당사 웹 사이트를 참조해주세요. 위의 두 행에서, 우리는 야생 말 클래스의 939개의 이미지와 Imagenet의 얼룩말 클래스 1177이미지에 대해 학습해 말과 얼룩말 사이의 개체 변환에 대한 결과를 보여줍니다. 말 $\rightarrow$ 얼룩말의 데모 비디오도 확인해 보세요. 가운데 두 줄은 Flickr의 요세미티의 겨울과 여름 사진에 대해 학습된 계절 변환에 대한 결과를 보여줍니다. 아래의 두 행에서, 우리는 ImageNet의 996개의 사과 이미지와 1020개의 오렌지 이미지에 대한 우리의 방법을 학습시켰습니다.
이 모델은 ImageNet에서 다른 객체 클래스로 변환하도록 학습합니다(각 클래스에는 약 1000개의 학습 이미지가 포함됨). Turmukhambetov은 한 개체를 동일한 범주의 다른 개체로 변환하는 하위 공간 모델을 제안하는 반면, 우리의 방법은 시각적으로 유사한 두 범주 간의 개체 변환에 중점을 둡니다.
Season transfer
위의 Figure 13에서 결과를 확인할 수 있으며 이 모델은 Flickr에서 다운로드한 Yosemite의 854장의 겨울 사진과 1273장의 여름 사진을 대상으로 학습되었습니다.
Photo generation from paintings
painting $\rightarrow$ photo 의 경우, 입력과 출력 사이의 색상 구성을 보존하기 위한 매핑을 장려하기 위해 추가 loss를 도입하는 것이 도움이 된다는 것을 발견했습니다. 특히, 우리는 Taigman의 기법을 채택했으며 target 도메인의 실제 샘플이 생성 모델에 대한 입력으로 제공될 때 생성 모델이 identity 매핑에 가까워지도록 정규화합니다. 즉, $\mathcal{L} _{\mathrm{identity}}(G, F) = \mathbb{E} _{y \sim p _{data}(y)}[|G(y)-y|_1] + \mathbb{E} _{x \sim p _{data}(x)}[|F(x)-x|_1]$ 입니다.

Figure 9: Monet의 painting $\rightarrow$ photo에 대한 identity mapping loss의 영향. 왼쪽에서 오른쪽까지 순서대로 : input, identity mapping loss가 없는 CycleGAN, identity mapping loss를 가진 CycleGAN. identity mapping loss는 입력된 그램의 색상을 보존하는 데 도움이 된다.
$\mathcal{L} _{\mathrm{identity}}$가 없으면 생성 모델 $G$와 $F$는 필요하지 않을 때 입력 영상의 색조를 자유롭게 변경할 수 있습니다. 예를 들어, 모네의 그림과 Flickr의 사진 사이의 매핑을 학습할 때, 생성 모델은 종종 낮의 그림과 일몰 동안 찍은 사진을 매핑할 수 있는데, 이런 매핑은 adversarial loss와 cycle consistency loss에서 동일하게 유효할 수 있기 때문이다. 이러한 identity mapping loss의 효과는 Figure 9에 나와 있습니다.

Figure 12: Monet의 그림을 사진 스타일로 매핑한 비교적 성공적인 결과입니다.
Figure 12에서 우리는 모네의 그림을 사진으로 변환하는 추가 결과를 보여줍니다. Figure 12와 Figure 9는 학습 셋에 포함된 그림에 결과를 보여주는 반면, 논문의 다른 모든 실험에 대해서는 테스트 셋 결과만 평가하고 보여줍니다. 학습 셋은 페어 데이터를 포함하지 않기 때문에 학습 셋의 그림에서 그럴듯한 변환을 생각해 내는 것은 중요한 작업입니다. 실제로 모네는 더 이상 새로운 그림을 그릴 수 없기 때문에 그림을 보이지 않는 “테스트 셋”으로 일반화하는 것은 시급한 문제가 아닙니다.
[정리]CycleGAN에서 이미지 색상을 보존하기 위해 추가로 identity loss를 사용할 수 있습니다.
cycle consistency loss가 $[\|G(F(y)) - y\|_1] + [\|F(G(x)) - x\|_1]$라면 identity loss는 $[\|G(y)-y\|_1] + [\|F(x)-x\|_1]$입니다. $G$는 데이터를 도메인 $Y$로 변환시키는 모델이므로 $y \in Y$인 $y$를 입력으로 주었을 때 변화하는 것이 없기를 바라고 마찬가지로 $F$는 데이터를 도메인 $X$로 변환시키는 모델이므로 $x \in X$인 $x$를 입력으로 주어도 변화가 없기는 바라는 것이 identity loss가 됩니다.
Photo enhancement

Figure 14: Photo enhancement : 스마트폰 스냅 사진 셋에서 전문적인 DSLR 사진으로 매핑된 시스템은 종종 얕은 초점을 생성하는 방법을 학습합니다. 여기서는 테스트 셋에서 가장 성공적인 결과 중 일부를 보여주며 평균 성능을 상당히 떨어집니다.
우리는 우리의 방법이 depth of field(DoF)가 더 낮은 사진을 생성하는 데 사용될 수 있음을 보여줍니다. 우리는 Flickr에서 다운로드한 꽃 사진으로 모델을 학습합니다. source 도메인은 스마트폰이 촬영한 꽃 사진으로 구성되는데, 보통 조리개가 작아 DoF가 깊습니다. target 도메인에는 조리개가 더 큰 DSLR로 캡처한 사진이 포함됩니다. 우리 모델은 스마트폰으로 찍은 사진에서 depth of field가 낮은 사진을 성공적으로 생성합니다.
Comparison with Gatys

Figure 15: 우리는 우리의 방법을 photo stylization에 대해 neural style transfer와 비교합니다. 왼쪽부터 오른쪽까지 순서대로 : input, 2개의 다른 대표적인 예술 작품을 스타일 이미지로 사용한 Gatys의 결과, 아티스트의 전체 컬렉션을 사용한 Gatys의 결과, CycleGAN
Figure 15에서, 우리는 photo stylization에 대한 neural style transfer과 우리의 결과를 비교합니다. 각 행에 대해 우리는 우선 neural style transfer의 스타일 이미지로 두 개의 대표적인 예술 작품을 사용합니다. 반면에 우리의 방법 전체 컬렉션 스타일의 사진을 생성할 수 있습니다. 전체 컬렉션의 neural style transfer와 비교하기 위해, 우리는 target 도메인에 걸쳐 average Gram Matrix를 계산하고 이 matrix를 사용해 Gatys과 함께 “average style”로 변환합니다.

Figure 16: 우리는 우리의 방법을 다양한 애플리케이션에서 neural style transfer과 비교합니다. 위에서 아래로 : 사과 → 오렌지, 말 → 얼룩말, 모네 → 사진. 왼쪽에서 오른쪽으로 : 입력 이미지, 두 개의 서로 다른 이미지를 스타일 이미지로 사용한 Gatys의 결과, target 도메인의 모든 이미지를 사용한 Gatys의 결과, CycleGAN
Figure 16은 다른 변환 작업들에 대한 유사한 비교를 보여줍니다. 우리는 Gatys는 원하는 출력과 밀접하게 일치하는 대상 스타일 이미지를 찾아야 하지만 여전히 사실적인 결과를 생성하지 못하는 경우가 많은 반면, 우리의 방법은 target 도메인과 유사하게 자연스럽게 보이는 결과를 생성하는 데 성공한다는 것을 관찰했습니다.
6. Limitations and Discussion

Figure 17: 우리의 방법에서 전형적인 실패 사례들. 왼쪽 : 개 $\rightarrow$ 고양이 변환 작업에서 CycleGAN은 입력에서 최소한의 변경만 만들어 낼 수 있었습니다. 오른쪽 : CycleGAN은 말 $\rightarrow$ 얼룩말 예제에서도 실패 사례가 나왔는데 모델이 학습 중 승마에 대한 이미지를 보지 못했지 때문입니다.
우리의 방법이 많은 경우에 설득력 있는 결과를 얻을 수 있었지만, 결과들이 모든 곳에서 긍정적인 결과인 것과는 거리가 있습니다. Figure 17은 몇 가지 실패 사례를 보여줍니다. 위에서 언급한 것들처럼 색상과 질감 변화를 수반하는 변환 작업에서 우리의 방법은 종종 성공적이였습니다. 우리는 기하학적 변화가 필요한 작업을 탐구했지만 거의 성공하지 못했습니다. 예를 들어 개 $\rightarrow$ 고양이(Figure 17, 좌측) 변환 작업에서 모델은 입력을 최소한의 변경만 하는 것으로 퇴화합니다. 이 실패는 외관 변경에 대한 우수한 성능을 위해 조정된 생성 모델 구조로 인해 발생할 수 있습니다. 더 다양하고 극단적인 변화, 특히 기하하적 변화를 다루는 것은 향후 작업에 중요한 문제입니다.
일부 실패 사례는 학습 데이터 셋의 분포 특성으로 인해 발생합니다. 예를 들어, 우리의 방법은 말 $\rightarrow$ 얼룩말 예시(Figure 17, 우측)에서 혼란스러워하는 모습을 보였는데, 이는 모델이 말이나 얼룩말을 타는 사람의 이미지를 포함하지 않은 ImageNet의 wild horse와 zebra에 대해 학습되었기 때문입니다.
우리는 또한 페어 데이터를 학습해 달성할 수 있는 결과와 페어를 이루지 않는 데이터를 사용한 방법으로 달성된 결과 사이의 지속적인 격차를 관찰했습니다. 어떤 경우에는 이 간격을 좁히기가 매우 어렵거나 심지어 불가능할 수도 있었습니다. 예를 들어, 우리의 방법은 때때로 photo $\rightarrow$ label 의 작업의 출력에서 나무나 빌딩의 label을 바꾸었습니다. 이 모호성을 해결하려면 어떤 형태로든 약간 semantic supervision이 필요할 수도 있습니다. 약한 지도 또는 준-지도 데이터를 통합하면 훨씬 더 강력한 변환 모델이 나올 수 있으며 준-지도 데이터를 여전히 완전 지도 시스템(fully-supercised system) 비용의 일부에 불과합니다.
그럼에도 불구하고, 많은 경우에 페어를 이루지 않은 데이터는 충분히 이용 가능하며 사용되어야 합니다. 본 논문은 “지도되지 않은” 환경에서 가능한 작업의 경계를 확장합니다.
[정리]색상, 질감 변화의 작업에는 성공적이였지만 외관 자체가 변화하는 것에는 성공하지 못했습니다. 또한 학습한 이미지 데이터 셋에 없던 객체가 이미지에 나타난다면 모델이 혼란스러워 하며 결과가 좋지 않음을 확인했습니다.
semantic segmentation과 같은 작업에서는 pix2pix 같이 페어를 이룬 데이터를 사용한 모델의 성능을 따라잡을 수 없었지만 준-지도 데이터 사용을 통해 성능 향상이 가능할 것으로 생각됩니다.
하지만 많은 경우에 페어를 이루지 않은 데이터를 사용해 모델이 좋은 결과를 내고 있으며 본 논문은 비 지도 환경에서 가능한 작업의 경계를 확장했다 할 수 있습니다.
모델의 구조가 소개되어 있는 Appendix 부분은 다음 글인 CycleGAN 논문 구현에서 구현 코드와 함께 소개해드리겠습니다.
끝까지 봐주셔서 감사합니다 :)
 solee
solee