SAGAN - 논문 리뷰
이번 논문은 self-attention을 Generative model에 적용한 SAGAN(Self-Attention Generative Adversarial Network)입니다. 사실 BIGGAN 논문을 보다 해당 논문이 SAGAN 모델을 바탕으로 한 걸 알게 되어서 SAGAN를 먼저 하게 되었습니다ㅎㅅㅎ
Self-Attention Generative Adversarial Network(SAGAN)은 convolution을 self-attention으로 대체해 long-range dependency 모델링이 가능하도록 제안된 모델입니다. 또한 spectral normalization과 TTUR을 사용해 Inception Score, Fréchet Inception Distance 모두에서 기존 State-of-the-art를 능가하는 성능을 보여주었습니다. SAGAN에 대해서 지금부터 살펴보겠습니다.![]()
소개
GANs는 ImageNet과 같은 multi-class를 모델링 시 문제를 가지고 있었습니다. 구조가 복잡한 클래스의 경우 생성 모델이 구조를 파악하지 못해 FID가 낮게 나오는 문제였습니다.

CGANS with Projectin Discriminator의 Figure 7.
당시 class conditional image generation task에서 SOTA인 CGANS with Projection Discriminator는 간헐천, 계곡과 같이 객체의 구조적 제약이 거의 없는 이미지(텍스처(질감)으로 구별 가능한 바다, 하늘과 같은 풍경) 생성은 탁월하지만, 하프, 크로스워드 등 일부 클래스(개와 같은 클래스의 이미지는 개의 털 텍스처(질감)은 성공적으로 생성되지만 일부 발이 생성되지 않는 경우가 발생)에서 기하학적/구조적 패턴을 파악하지 못합니다. 실제로 위 논문의 Figure 7에서 풍경의 FID는 낮지만 객체에 대한 FID는 높은 것을 확인할 수 있습니다.
FID(Fréchet Inception Distance)
Fréchet Inception Distance(FID)는 생성 모델에서 생성된 이미지의 품질을 평가하는 데 사용되는 metric으로 Inception Score(IS)를 개선하기 위해 제안되었습니다. 두 분포의 거리를 계산하는 metric으로 값이 낮을 수록 분포가 가까워 생성 이미지가 실제 이미지와 유사함을 의미해 FID 점수가 낮을 수록 좋습니다.FID를 계산하기 위해서 우선 pretrain된 Inception V3를 사용해 실제 이미지와 생성된 이미지의 (2048, ) 크기의 feature map을 계산합니다. 계산된 이 feature map들의 분포 차이를 계산하기 위해 정규분포(Gaussian distribution)를 사용합니다. 정규분포는 평균과 분산이 주어져 있을 때 엔트로피를 최대화하는 분포이므로 다차원 정규분포를 따른다고 가정해 두 feature map의 평균(mean)과 공분산(covariance) 차이를 이용해 두 분포의 차이를 계산합니다. 이때 차이는 Wasserstein-2 distance라고도 불리는 Fréchet distance로 계산합니다. 아래 수식이 Fréchet distance를 활용한 FID의 수식입니다.
$ d^2((m,C),(m_w, C_w)) = \| m-m_w \|^2_2 + Tr(C + C_w - 2(CC_w)^{1/2}) $
$m$, $C$는 실제 이미지의 feature map의 평균과 공분산이고 $m_w$, $C_w$는 생성된 이미지의 feature map의 평균과 공분산이며, Tr은 행렬의 대각합(trace)를 의미합니다.
참고
- 페이오스님의 GAN 평가지표
- viriditass.log님의 GAN은 알겠는데, 그래서 어떤 GAN이 더 좋은건데?
이에 대한 가능한 설명은 모델이 서로 다른 이미지 영역에 걸쳐 종속성(dependency)를 모델링하기 위해 convolution에 크게 의존한다는 것입니다. convolution은 receptive field가 local에 해당하므로 long range dependency를 위해서는 여러 convolution 레이어를 통과한 후에만 처리할 수 있습니다.
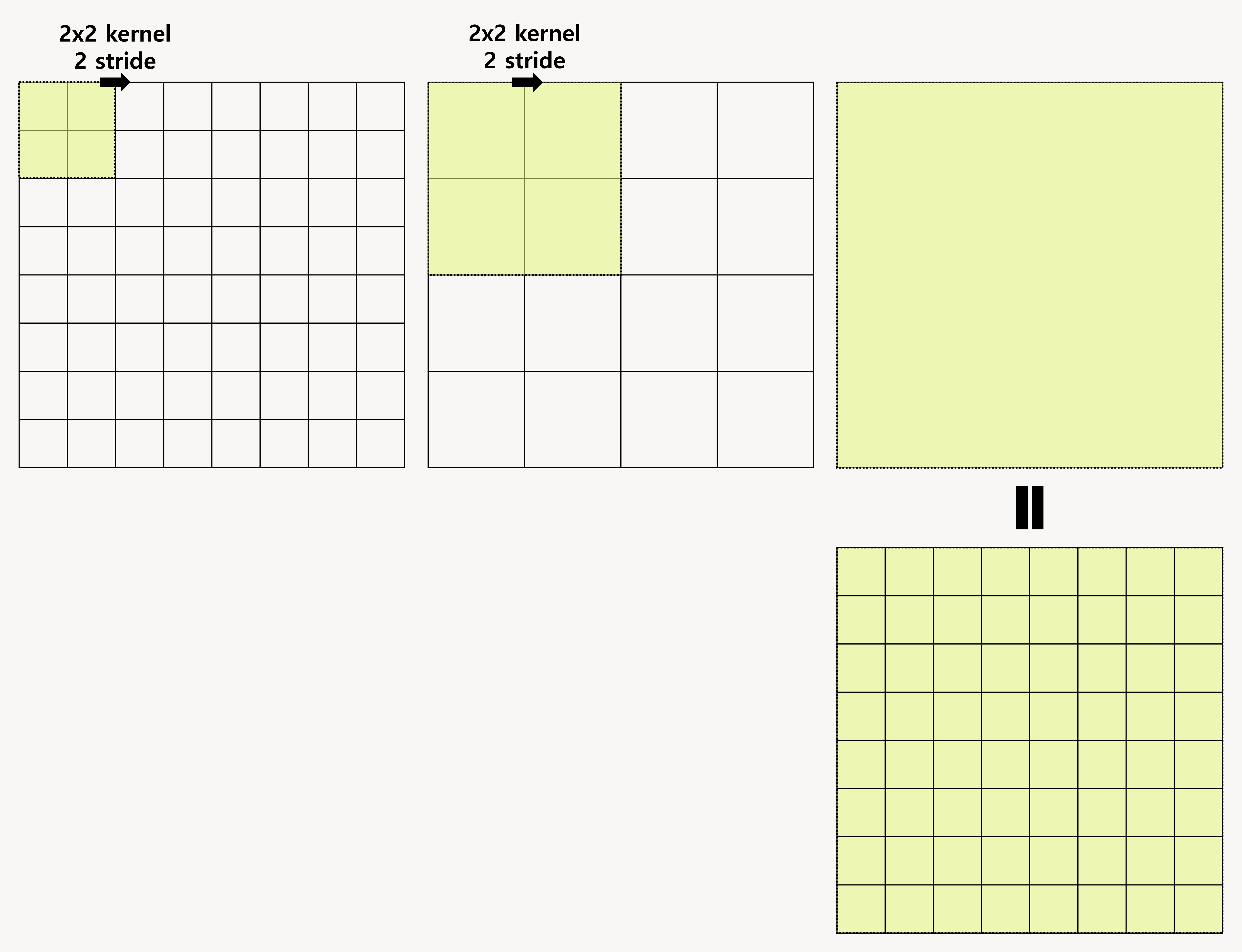
convolution이 1 layer가 깊어질수록 kernel 크기가 곱해진만큼을 커버할 수 있는 것을 볼 수 있습니다.
따라서 작은 모델들은 layer 수가 작아 long range dependency 표현 자체가 어렵습니다. 모델이 아닌 최적화 알고리즘을 사용해서도 long range dependency를 포착하도록 할 수 있겠지만 이를 위한 파라미터 값을 발견하기 어려울 뿐만 아니라 이 경우 새로운 입력에 대해 실패하기도 쉬워집니다. convolution의 local을 키우기 위해 convolution kernel의 크기를 증가시키면 receptive field가 커지니 네트워크의 표현 용량을 증가시킬 수 있지만 local convolutional 구조를 사용해 얻은 계산 및 통계의 효율성이 손실됩니다.
따라서 논문에서는 Self-Attention을 도입한 Self-Attention Generative Adversarial Networks(SAGANs)를 제안합니다. self-attention module은 모든 위치에서 feature의 가중치 합으로 위치 반응을 계산하며, attention vector는 적은 비용으로 계산이 가능하기에 long range dependency와 통계 효율성 사이의 더 나은 균형을 보여줍니다.
self-attention 외에도, conditioning(조건)에 대한 기술을 추가합니다. Is Generator Conditioning Causally Related to GAN Performance?는 well-condition 생성 모델이 더 나은 성능을 보이는 경향을 보여주었는데, 더 좋은 conditioning을 위해 Spectral Normalization for Generative Adversarial Networks에서 판별 모델에만 적용되었던 spectral normalization 기술을 생성 모델에 적용합니다.
제안된 방법들로 Inception score의 최고점을 36.8에서 52.52로 높였고 Fréchet Inception Distance를 27.62에서 18.65로 줄임으로써 이전 SOTA를 능가함을 보여주었다 합니다.
Self-Attention
SAGAN을 이해하기 위해 논문의 이름에도 들어가 있는 Self-Attention에 대해서 살펴보겠습니다. Self-Attention은 Attention Is All You Need에서 소개되었던 개념으로 RNN의 long term dependency 문제를 해결하기 위해 제안되었으나 SAGAN에서는 image generation task에 Self-Attention을 사용해 long range dependency를 해결하고자 합니다.
Self-attention은 입력 값 일부에 대해 입력 값 전체에 대한 관계를 계산합니다. 자연어라면 단어 하나와 전체 텍스트가 임베딩된 벡터 전체, 이미지처리라면 픽셀 하나와 이미지 전체가 임베딩된 feature map 사이의 관계를 계산하는 것이 됩니다. 입력 값 일부가 입력 값 전체에 대해 관계를 계산하는 것을 모든 입력에 대해 계산해 각각의 값들이 다른 값들과 얼마나 관련되어 있는지 입력값 내의 연관성을 계산할 수 있게 됩니다.
RNN처럼 들어온 입력 시간 순대로 계산한다거나, CNN의 Convolution처럼 입력값 일부를 사용하는 것이 아닌 모든 입력에 대해 한번에 계산하기 때문에 local dependency가 아닌 long range dependency 모델링이 가능합니다.

Figure 1. 각 행에서 첫번째 이미지는 색상이 지정된 점이 있는 5개의 대표적인 쿼리 위치를 보여줍니다. 나머지 5개의 이미지는 해당 쿼리 위치에 대한 attention map으로 해당 색상으로 표시된 화살표가 가장 주의(attention)를 기울이는 지역을 보여줍니다.
이를 위해서 입력 값을 key, query, value로 나뉘어 계산해 사용합니다. key 값은 입력 값 전체, query는 입력 값의 일부, value는 각각의 입력 값들이 가지고 있는 실제 값을 의미합니다.위의 Figure 1는 생성된 이미지(1열)의 여러 색상의 5개의 점이 query에 해당합니다. 2~5열은 각각의 query인 점들에 대해 모든 key(모든 픽셀)와 관계를 계산한 attention map을 보여주는데 밝은 부분은 query와 해당 위치의 key의 관련이 깊다는 것을 의미합니다. self-attention은 attention map과 실제 값을 의미하는 value의 곱으로 구할 수 있으며 Attention Is All You Need에서 attention을 구하는 수식은 아래와 같습니다.
\[Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V\]수식으로는 잘 와닿지 않으니 제가 이해한 대로 이미지 feature map이 입력으로 들어왔을 때를 그림으로 나타내 보았습니다.
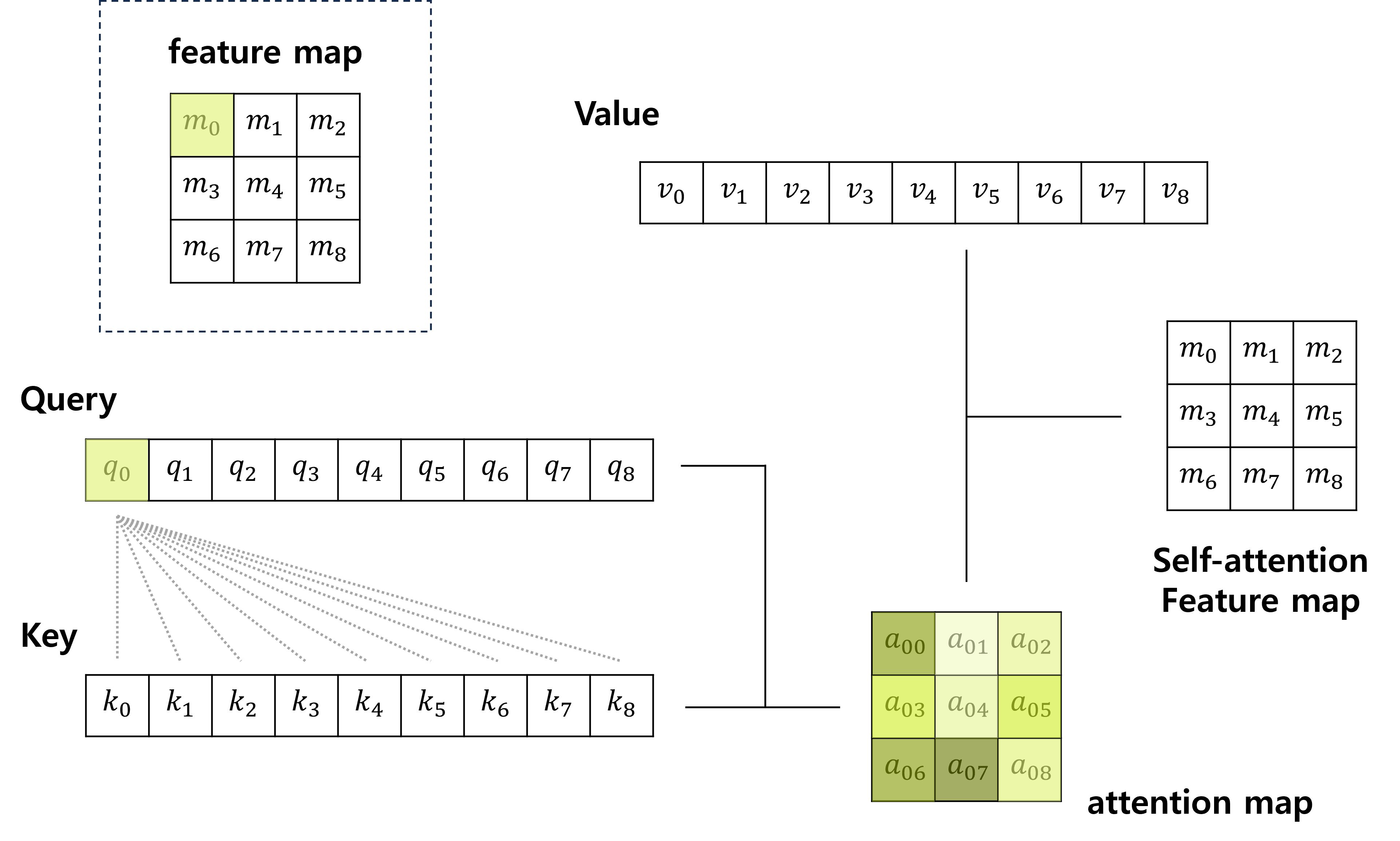
feature map이 입력으로 들어오면 해당 feature map으로 Query, Key, Value 각각을 1x1 convolution으로 계산합니다. 그림에서는 query로 $q_0$을 선택하고 모든 key 값과 계산을 통해 $q_0$과의 attention 정도를 나타내는 attention map을 구합니다(실제로는 행렬곱을 통해 모든 query과 key를 한번에 계산합니다). 계산된 attention map을 시각화하면 Figure 1과 같이 query인 값과 key 값들의 연관된 정도에 따라 다른 밝기 수준을 가지고 있어 어떤 픽셀과 관련이 있는지 시각화가 가능합니다. 이후 Value와 행렬곱 계산을 통해 Self-attention feature map을 계산합니다.
이제 SAGAN 논문에서 Attention 설명이 된 Figure를 살펴보고 차이에 대해 알아보겠습니다.
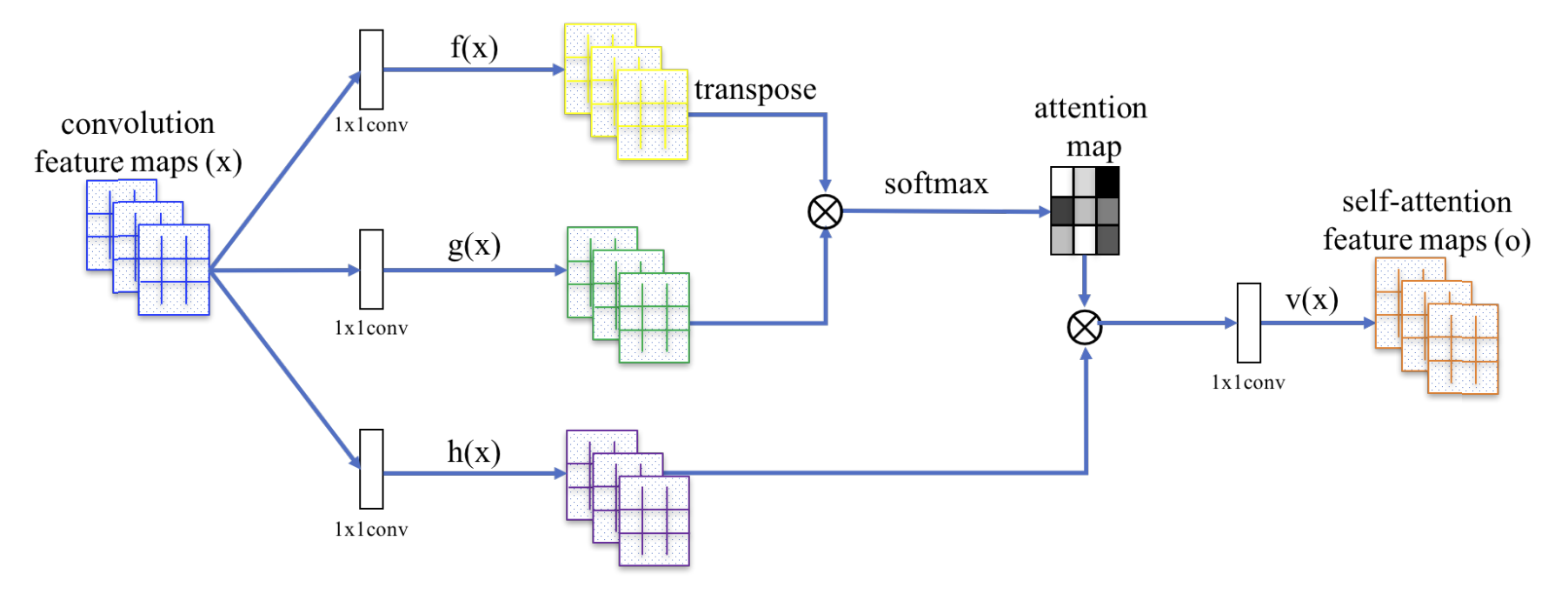
Figure 2. SAGAN의 self-attention 모듈. $\otimes$는 행렬 곱을 나타내며, softmax 연산은 각 행에 대해 수행됩니다.
convolution layer를 통과한 feature map($x$)를 입력으로 받아 key에 해당하는 $f(x)$, query에 해당하는 $g(x)$와 value에 해당하는 $h(x)$를 각각 입력 값 $x$에 kernel_size=1인 1x1 convolution으로 계산합니다.
attention map은 key와 query의 행렬 곱에 softmax 연산을 취해 아래와 같이 계산할 수 있습니다.
\[\beta _{j, i} = \frac{exp(s _{ij})}{\sum ^N _{i=1}exp(s _{ij})}, \text{ where } s _{ij} = \mathbf{f}(\mathbf{x_i})^T \mathbf{g}(\mathbf{x_j})\]attention map은 픽셀 간의 관계를 나타내는데, 수식의 $\beta _{j, i}$는 $j$번째 영역을 합성 할 때 모델이 $i$번째 위치에 어느 정도 관심을 기울이는지를 나타냅니다.

Figure 5. attention map의 시각화로 이미지들은 SAGAN에 의해 생성되었습니다.
출력 픽셀에 가장 근접하고 해석하기 가장 직관적인 생성 모델의 마지막 layer에 있는 attention map을 시각화했습니다.
각 셀에서, 가장 첫번째 이미지는 색상이 지정된 점이 있는 4개의 대표적인 쿼리 위치를 보여줍니다. 다른 4개의 이미지들은 해당 쿼리 위치에 대한 attention map으로, 해당 색상으로 표시된 화살표는 가장 많이 주의를 기울인 영역을 보여줍니다.
우리는 네트워크가 단순히 공간적 인접(adjacency)이 아닌 색상과 질감의 유사성에 따라 attention을 할당하는 것을 학습한다는 것을 관찰했습니다.
SAGAN에서 다양한 이미지에 생성 모델의 attention weight를 시각한 결과를 Figure 5에서 확인할 수 있습니다.
계산한 attention map과 value인 $h(x)$를 곱한 후 1x1 convolution을 한번 더 취해 self-atten feature maps $o$를 계산합니다. Attention Is All You Need에서 Attention의 계산법은 $Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$ 였다면 SAGAN에서는 $v(x)$인 1x1 convolution이 하나 추가되어 계산하는 것이 차이입니다.
\[\mathbf{o_j} = \mathbf{v} \left ( \sum^N_{i=1}\beta_{j, i}\mathbf{h}(\mathbf{x_i}) \right ), \mathbf{h}(\mathbf{x_i}) = \mathbf{W_h x_i}, \mathbf{v}(\mathbf{x_i}) = \mathbf{W_v x_i}.\]최종 결과는 계산한 self-attention feature map인 $o$와 입력 값 $x$를 더해 출력합니다. 이때 학습 가능한 스칼라 값으로 0으로 초기화된 $\gamma$를 $o$에 곱해 self-attention feature map의 크기를 계산하는데, 논문에서는 학습 가능한 $\gamma$를 사용함으로써 네트워크가 처음에는 local 주변의 신호에 의존하다 점차 학습이 진행되며 non-local 신호에 더 많은 가중치를 부여하는 방법을 학습할 수 있다고 합니다. 논문에서 $\gamma$를 0으로 초기화한 것에 대해서는 직관으로 쉬운 일을 먼저 학습하고 복잡성을 점진적으로 증가시켜 학습하기를 원했기 때문이라고 설명합니다..
\[\mathbf{y_i} = \gamma \mathbf{o_i} + \mathbf{x_i}\]SAGAN의 Self-Attention에 대해 간단하고 명료하게 표현한 코드가 있어 가져왔습니다.
class Self_Attention(nn.Module):
def __init__(self, inChannels, k=8):
super(Self_Attention, self).__init__()
embedding_channels = inChannels // k # C_bar
self.key = nn.Conv2d(inChannels, embedding_channels, 1)
self.query = nn.Conv2d(inChannels, embedding_channels, 1)
self.value = nn.Conv2d(inChannels, embedding_channels, 1)
self.self_att = nn.Conv2d(embedding_channels, inChannels, 1)
self.gamma = nn.Parameter(torch.tensor(0.0))
self.softmax = nn.Softmax(dim=1)
def forward(self,x):
"""
inputs:
x: input feature map [Batch, Channel, Height, Width]
returns:
out: self attention value + input feature
attention: [Batch, Channel, Height, Width]
"""
batchsize, C, H, W = x.size()
N = H * W # Number of features
f_x = self.key(x).view(batchsize, -1, N) # Keys [B, C_bar, N]
g_x = self.query(x).view(batchsize, -1, N) # Queries [B, C_bar, N]
h_x = self.value(x).view(batchsize, -1, N) # Values [B, C_bar, N]
s = torch.bmm(f_x.permute(0,2,1), g_x) # Scores [B, N, N]
beta = self.softmax(s) # Attention Map [B, N, N]
v = torch.bmm(h_x, beta) # Value x Softmax [B, C_bar, N]
v = v.view(batchsize, -1, H, W) # Recover input shape [B, C_bar, H, W]
o = self.self_att(v) # Self-Attention output [B, C, H, W]
y = self.gamma * o + x # Learnable gamma + residual
return y, o
Loss
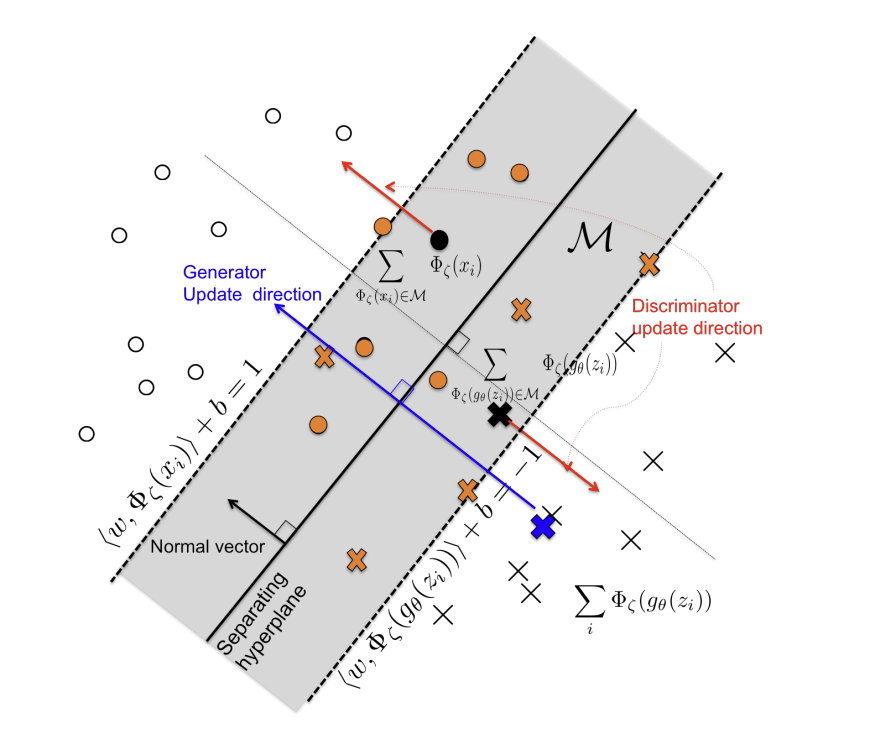
SVM hyperplane을 사용한 Geometric GAN. 판별 모델은 빨간 화살표의 방향으로, 생성 모델은 파란 화살표의 방향으로 업데이트됩니다.
Adversarial loss는 hinge loss를 사용합니다. hinge loss는 보통 SVM에서 사용되었는데 Geometric GAN에서 SVM의 hyperplane을 GAN에 적용했습니다. 위의 그림에서 좌측 상단 부분이 실제 데이터($O$), 우측 하단이 생성된 가짜 데이터($X$)들로 모여있으며 hyperplane으로 판별 모델이 데이터를 판별하는 것을 볼 수 있습니다.
Geometric GAN의 판별 모델 $D$는 최적의 hyperplane을 찾기 위해 soft-margin 내의 판별 오차들에 대해 학습합니다. 실제 데이터 $O$의 판별 값이 1 미만인 경우와 생성된 가짜 데이터 $x$의 판별 값이 -1 이상인 경우, 즉 $-1 < D(G(z), y)$ 또는 $D(x,y) < 1$인 경우 hyperplane(0)에서 멀어지도록 모델을 업데이트해 margin을 최대화하도록 만듭니다.
생성 모델은 이런 판별 모델과 반대로 hyperplane에 근접한 데이터 $G(z)$를 생성하도록 업데이트됩니다. 판별 모델은 데이터의 판별값이 $G(x) >= 1, G(z) <= -1$이 되도록 만드니 판별값의 절대값이 커지도록 만든다면 생성 모델은 데이터의 판별값의 절대값이 작아지도록 만드는 것이 목표입니다.
위의 수식이 SAGAN에서 사용하는 adversarial hinge loss입니다. 판별 모델 $D$의 경우 $(x, y) ~ p_{data}$인 실제 데이터 $(x, y)$를 입력으로 받는다면 $D(x, y) < 1$인 경우 1 이상의 값을, 생성 모델이 생성한 $G(z)$를 입력으로 받는다면 $D(G(z), y) > -1$인 경우 출력으로 -1 이하의 값을 만들어 판별값의 절대값이 커지도록(hyperplane에서 멀어지도록) 업데이트하는 것이 목표입니다. 반대로 생성 모델 $G$는 $G$가 생성한 이미지 $G(z)$를 $D$에게 입력으로 준 결과가 hyperplane에 가까워지도록 만드는 것이 이상적입니다.
이 hinege loss는 SAGAN 논문 뿐만 아니라 state-of-the-art 논문으로 SAGAN과 비교하기 위한 baseline 모델인 CGANS with Projection Discriminator 또한 adversarial loss로 hinge loss를 사용했습니다.
Stabilize
GANs 학습을 안정화하기 위해 Spectral normalization과 Two Time Scale Update Rule(TTUR)을 사용합니다.
Spectral Normalization
Spectral Normalization은 Spectral Normalization for Generative Adversarial Networks에서 GANs 학습 안정화를 위해 판별 모델에 적용되었습니다. 각 layer의 spectral norm을을 특정 상수로 제한하는 것으로 판별 모델의 Lipschitz 상수를 제한하는 방법으로 모든 가중치 레이어의 spectral norm은 1로 설정하는 것이 지속적으로 잘 수행되기 때문에 다른 normalization 방법과 비교해 추가적인 hyperparameter 튜닝을 필요로 하지 않는다 합니다. 또한 계산 비용이 적은 것이 장점입니다.
SAGAN은 생성 모델에도 Spectral normalization을 적용하는 것으로 생성 모델의 파라미터 크기의 상승을 방지하고 비정상적인 gradient를 피할 수 있어 Spectral normalization을 생성 모델과 판별 모델 모두에 적용합니다. 이후 생성 모델과 판별 모델 모두의 Spectral normalization이 안정적인 학습을 보여줄 뿐만 아니라 생성 모델 업데이트 당 판별 모델 업데이트 수를 더 적게 만드는 것이 가능해 학습에 대한 계산 비용을 크게 감소시킨다는 것을 발견했습니다. SAGAN은 판별모델의 learning rate는 0.0004로, 생성 모델의 learning rate는 0.0001을 사용해 판별 모델과 생성 모델 업데이트 비율을 1:1로 학습합니다.
TTUR
Two Time-Scale Update Rule(TTUR)은 GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium에서 제안한 방법으로 생성 모델과 판별 모델에 별도의 learning rate를 사용하는 방법입니다. 판별 모델 학습 : 생성 모델 학습 = 5 : 1과 같이 판별 모델의 느린 학습 문제를 보완하기 위해 SAGAN에서는 TTUR을 사용했습니다. TTUR을 사용해 판별 모델 학습 : 생성 모델 학습 = 1 : 1로 학습이 가능하며 판별 모델의 학습 step 수를 더 적게 사용하므로 동일한 시간에서 더 나은 결과를 얻고자 했습니다.
결과
정략적 평가를 위해 논문에서는 conditional class 분포와 marginal class 분포 사이의 KL divergence를 계산하는 Inception score와 생성된 이미지와 실제 이미지의 Inception-v3의 feature space의 Wasserstein-2 distance를 계산하는 FID, 각 class 내의 생성된 이미지와 실제 이미지 사이를 비교하는 Intra FID를 계산합니다.
SAGAN 모델은 128x128 이미지를 생성하도록 설계되었으며, Spectral normalization은 생성 모델과 판별 모델에 모두 사용되었습니다. TTUR을 사용하기 때문에 판별 모델의 learning rate는 0.0004이고 생성 모델의 learning rate는 0.0001로 설정되었으며 Adam optimizer(β1 = 0 and β2 = 0.9)를 사용했다 합니다.
Spectral & TTUR
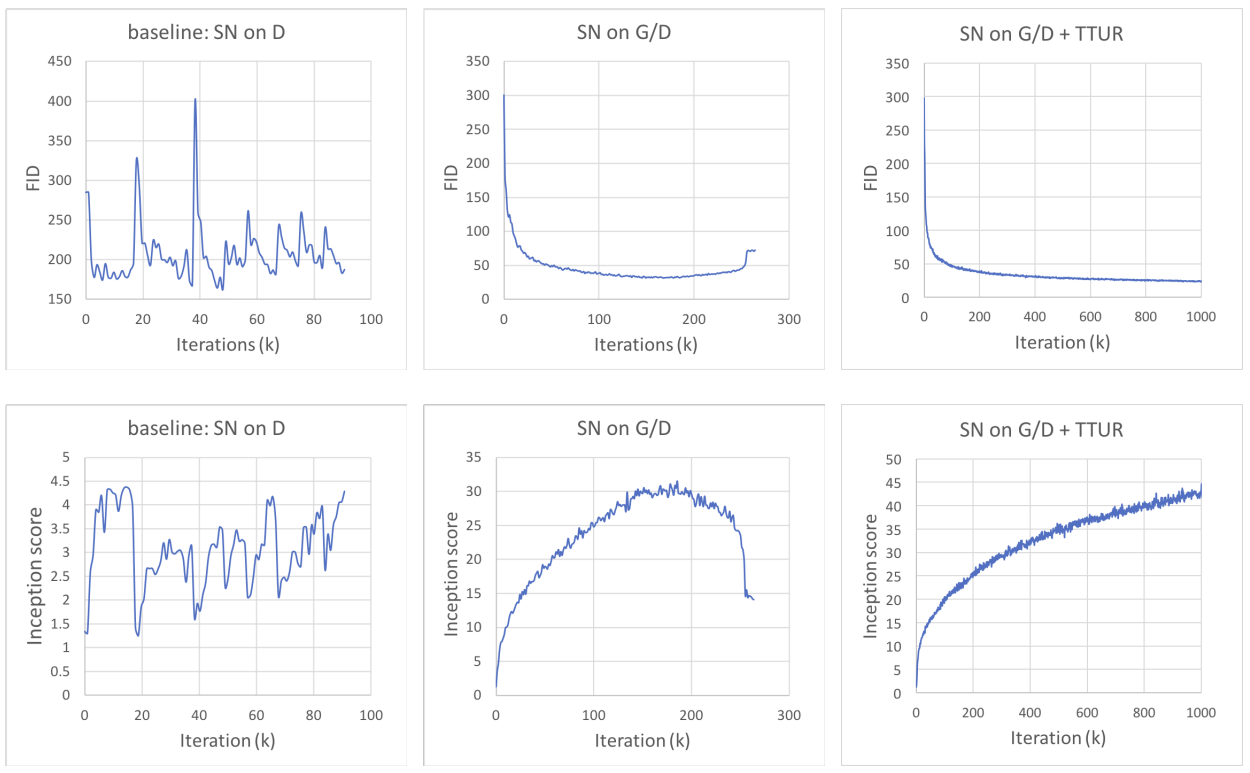
Figure 3. 제안된 안정화 기술인 “SN on $G/D$”와 two time scale learning rates(TTUR)을 사용한 SAGAN과 baseline 모델의 학습 곡선(Training curve). 모든 모델은 $G$와 $D$에 대해 1:1 균형 업데이트를 사용해 학습됩니다.

Figure 4. baseline 모델과 SAGAN 모델에서 “SN on $G/D$”와 “SN on $G/D$ + TTUR”로 무작위 생성된 128x128 결과
생성 모델과 판별 모델에 Spectral normalizatiokn(SN)을 적용하고 불균형한 learning rate(TTUR)을 적용해 제안된 안정화 기술의 효과를 평가하기 위한 실험을 진행합니다. SN on G/D와 SN on G/D + TTUR은 당시 SOTA로 baseline으로 사용된 CGANS with Projection Discriminator와 비교되며 이 baseline 모델은 SN이 판별 모델에만 사용되었기에 baseline: SN on D로 표시됩니다.
판별 모델 $D$과 생성 모델 $G$에 대해 1:1, 즉 한번씩 번갈아가면서 학습을 하면 Figure 3의 가장 왼쪽 하단의 그림과 같이 학습이 매우 불안정해지며 학습 초기에 mode collapse를 보여줍니다. Figure 4의 가장 왼쪽 상단의 그림은 10k iteration에서 baseline 모델에 의해 무작위로 생성된 일부 이미지를 보여줍니다. 원본 논문에서 이런 불안정한 학습 동작들은 $D$와 $G$의 학습 비율을 5:1로 설정해 크게 완화할 수 있지만, 그만큼 학습 시간이 길어지게 됩니다. 제안된 기술은 1:1 학습을 하기 때문에 동인한 시간이 주어졌을 때 모델이 더 나은 결과를 얻을 수 있습니다.
Figure 3의 중간 하단 그림에서 볼 수 있듯이, 생성 모델과 판별 모델에 SN을 적용해 1:1 학습을 진행했을 때 SN on G/D가 크게 안정화되었습니다. 그러나 학습 중 결과의 품질이 계속해서 좋아지지만은 않으며 260k iteration에서 FID와 IS가 떨어지기 시작합니다. Figure 4의 SN on G/D의 160k의 FID 값은 33.39였지만 SN on G/D의 260k의 FID값은 72.41로 오히려 결과 이미지의 품질이 떨어짐을 볼 수 있습니다.
하지만 Spectral normalization 뿐만 아니라 생성 모델과 판별 모델에 다른 learning rate(TTUR)을 사용해 학습시킨 SN on G/D + TTUR에 의해 생성된 이미지의 품질은 전체 학습 과정 동안 계속해서 향상되어 1M iteration 동안 결과 품질이나 FID 또는 Inception score의 현저한 감소를 관찰되지 않아 정량적, 정성적 결과 모두 GAN에 Spectral normalization과 TTUR을 적용해 1:1 업데이트로 학습하는 것이 안정화에 효과적이라 할 수 있습니다. 또한 두 기법 모두 어떤 모델이던 부가적으로 적용할 수 있는 기술이므로 논문의 이후 실험들에는 생성 모델과 판별 모델에 모두 Spectral normalization과 TTUR을 사용해 1:1 업데이트로 학습했습니다.
Self-attention

Table 1. GANs에서 Self-Attention과 Residual block의 비교.
모든 모델들은 100만번 iteration으로 학습되었으며 최고의 Inception Score(IS)와 Fréchet Inception Distance(FID)를 확인할 수 있습니다. $feat_k$은 kxk feature map에 block을 추가하는 것을 의미합니다.
Self-attention mechanism의 효과를 확인하기 위해 feature map 크기에 따라 Self-attention을 적용해 비교합니다. 8x8 크기와 같이 feature map이 작은 경우 feature map이 작기 때문에 self-attention이 local convolution과 유사한 역할만을 수행하게 되고 feature map이 커질 경우 더 많은 condition을 선택할 수 있기 때문에 long-range dependency 모델링이 가능해지게 되며 FID 값도 향상됨을 볼 수 있습니다.
동일한 파라미터의 상태에서 self-attention block은 residual block과 비교해 더 나은 결과를 얻을 수 있음을 볼 수 있습니다. 8x8 feature map에서 self-attention을 residual block으로 교체하면 학습이 안정적이지 않아 성능이 크게 저하되고 FID 값이 22.98에서 42.13으로 증가합니다. 학습이 순조롭게 진행되는 32x32 feature map에서도 self-attention block을 residual block으로 교체하면 FID와 Inception score가 더 나쁜 결과를 보여줌을 통해 SAGAN을 사용해 성능이 향상되는 것이 단순히 모델 깊이와 용량의 증가 때문이 아님을 알 수 있습니다.
SOTA와 비교

Table 2. ImageNet에서 class conditional 이미지 생성을 위해 제안된 SAGAN과 state-of-the-art GAN 모델(Odena et al., 2017; Miyato & Koyama, 2018)의 비교.
당시 ImageNet의 class conditional 이미지 생성의 state-of-the-art GAN 모델인 CGANS with Projection Discriminator(SNGAN-projection)와 Conditional GAN 모델인 AC-GAN과 Inception Score, Intra FID, FID를 비교한 결과를 Table 2에서 확인하실 수 있습니다. SAGAN은 3 종류의 metric에서 모두 최고를 달성했습니다.

Figure 6. 여러 클래스에 대해 SAGAN이 생성한 128x128 이미지 예시들.
각 행은 하나의 클래스에 대한 예시를 보여줍니다. 왼쪽 끝의 열은 SAGAN(left)와 state-of-the-art 방법(Miyato & Koyama, 2018)(right)의 intra FID가 나열되어 있습니다.
Figure 6은 ImageNet의 대표적인 클래스에 대한 생성된 이미지를 보여줍니다. SAGAN은 금붕어(goldfish), 세인트버나(saint bernard)와 같이 복잡한 기하학적, 구조적 패턴을 가진 클래스를 합성하기 위해 CGANS with Projection Discriminator(SNGAN-projection)보다 Intra FID 점수가 낮아 더 나은 성능을 보임을 확인할 수 있습니다. 하지만 반대로 질감으로 구별될 수 있어 기하학적, 구조적 패턴이 거의 없는 돌담(stone wall), 산호 곰팡이(coral fungus)의 경우 오히려 성능이 낮다는 것 또한 확인할 수 있습니다.
SAGAN은 기하학적, 구조적 패턴에 강해 self-attention mechanism을 long-range global dependency를 포착하기 위해 convolution과 같이 사용해 상호 보완적으로 작동해 좋은 결과를 이끌어 내지만, 단순 텍스처에 대한 dependency의 경우 local convolution과 유사한 역할을 해 좋은 결과를 이끌어 내지 못한다고 합니다.
SAGAN 논문 리뷰글의 끝입니다. 끝까지 봐주셔서 감사합니다:)
학습까지 코드 짜서 돌려보면 좋겠지만 제 데탑에서는 돌아가지 않을 거 같아서 일단 코드글은 미뤄둘까 합니다. GPU 신청을 해놓은 게 있는데, 신청 성공하면 그때 돌려볼 수 있을 것 같습니다. 제발! 되기를!
 solee
solee