GAN(2) - 논문 구현

0. 소개

gan의 코드 구현 글입니다:)
논문에 언급된 부분들을 구현하고 그 외의 부분들은 기본적인 MLP 방식을 사용했습니다.
이전 글인 gan(1) - 논문 분석 글을 본 후 이 글을 보시는 걸 추천드립니다!

1. 데이터

데이터셋은 MNIST 데이터셋을 사용했습니다. torchvision에서 코드를 통해 다운받고 쓸 수 있으니 따로 다운받으실 필요없이 편하게 사용할 수 있습니다.
다만 다운받았을 때 torchvision의 데이터는 PIL.Image.Image타입으로 들어오게 됩니다. Tensor로 변경하기 위해 transform 부분 코드를 넣어 데이터 타입을 변경해주었습니다.

dataloader = DataLoader(
    datasets.MNIST('/content/drive/MyDrive/Colab Notebooks/gan/data',
                   train=True,
                   download=True,
                   transform=transforms.Compose([transforms.ToTensor()])),
    batch_size=batch_size,
    shuffle=True,
    drop_last=True)

plt를 이용해 데이터 이미지와 라벨을 출력해 제대로 데이터가 들어왔는지 확인해봅시다!
dataloader에서 batch_size만큼의 데이터를 next(iter)를 통해 받아온 후 fig를 통해 출력해보았습니다.

images, labels = next(iter(dataloader))

fig = plt.figure(figsize=(8, 8))
for idx in range(4):
  image = images[idx]
  label = labels[idx]

  fig.add_subplot(1, 4, idx+1)
  plt.axis('off')
  plt.title(label)
  plt.imshow(image[0], cmap='gray')

fig.tight_layout()
plt.show()

mnist
원하던 mnist의 이미지와 라벨이 들어온 것을 확인했습니다:)

2. 모델

2.1. Generator

generator의 경우 논문에서 rectifier linear activation(relu), sigmoid activation을 사용했다 언급되어 있습니다. 따라서 마지막 activation은 sigmoid 그 외의 activation은 relu를 사용하도록 모델을 구현했습니다.
generator는 입력 노이즈의 크기인 (28, 28)과 같은 크기의 결과 이미지를 생성하는게 목적이므로 마지막 Linear는 784(28x28)로 고정해주었습니다.

class Generator(nn.Module):
  def __init__(self, z_dim=100, img_shape=(28,28)):
    super(Generator, self).__init__()

    self.z_dim = z_dim
    self.img_shape=img_shape

    self.model = nn.Sequential(
        nn.Linear(self.z_dim, 256),
        nn.ReLU(),
        nn.Linear(256, 512),
        nn.ReLU(),
        nn.Linear(512, 784),
        nn.Sigmoid()
    )

  def forward(self, z):
      img = self.model(z)
      img = img.view(img.size(0), *self.img_shape)
      return img

2.2. Discriminator

discriminator의 경우 논문에서 maxout activation과 dropout을 사용했다 언급되어 있습니다.
maxout은 Generative Adversarial Networks의 저자인 Ian J. Goodfellow의 이전 논문인 Maxout Networks에서 나온 maxout unit이라 불리는 activation입니다. dropout의 효과를 극대화하기 위해 사용하며 파라미터의 수를 정할 수 있는 것이 특징입니다.

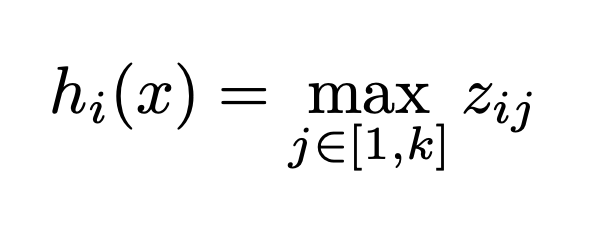
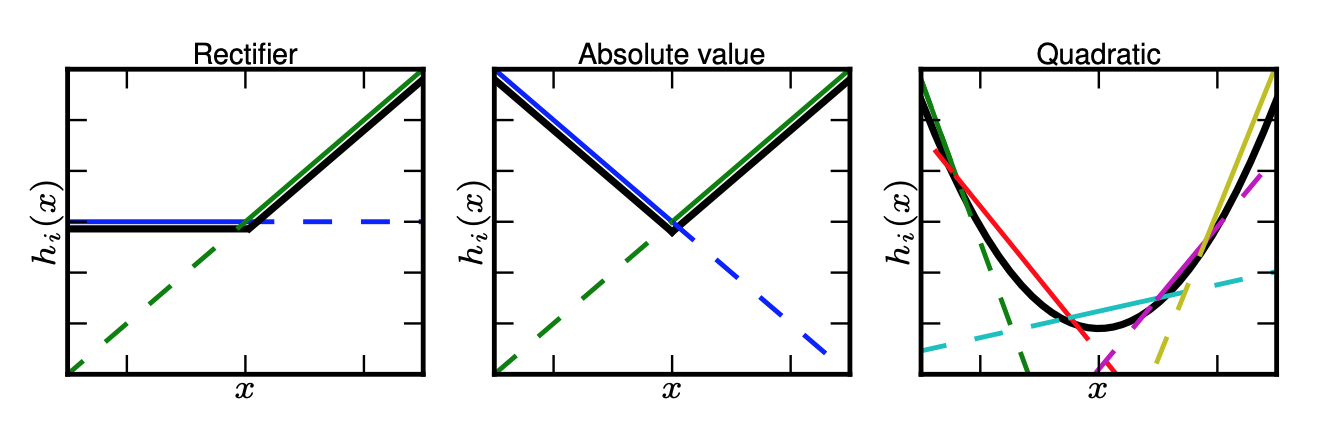
maxout의 수식에서 $k$가 사용자가 지정할 수 있는 파라미터의 수입니다. 오른쪽 그림의 Rectifier와 Absolute value로 표시된 그래프은 $k = 2$인 경우이고 Quadratic으로 표시된 그래프는 $k = 4$인 경우입니다.

오른쪽 그림을 보면 $h_i(x)$의 이해가 쉬워집니다. maxout은 사용자가 지정한 $k$개수만큼 직선을 만들고 만들어진 직선 값들 중 최대값을 취합니다. 이때 직선(z)의 방정식은 $z = x^TW+b$이며 $W$와 $b$는 학습 과정 중 값이 변하는 파라미터입니다. 수식대로 maxout을 구현해보겠습니다:)

class Maxout(nn.Module):
  def __init__(self, k=3):
    super(Maxout, self).__init__()

    self.k = k

    self.weight = torch.randn(self.k, requires_grad=True).unsqueeze(1).cuda()
    self.bias = torch.randn(self.k, requires_grad=True).unsqueeze(0).cuda()

  def forward(self, input):
    x = input.flatten().unsqueeze(1)
    x = nn.functional.linear(x, self.weight, self.bias)
    x = nn.functional.max_pool1d(x, self.k)
    x = x.reshape(*input.shape)
    return x

우선 직선의 개수인 $k$를 입력으로 받을 수 있도록 했습니다. $k$의 수만큼 직선을 만들어야 하므로 $k$개의 weight와 bias를 생성하게 됩니다.

forward 함수에서는 입력으로 받은 이미지를 flatten 함수로 펼치고 linear 함수로 연산을 합니다. 이때 nn.functional.linear 함수는 입력으로 받은 x, weight($A$), bias($b$)로 $y = xA^T+b$ 값을 출력합니다. linear 함수를 통해 input 값들의 직선 값을 계산할 수 있습니다.

다음으로 max_pool1d 함수를 적용합니다. max_pool1d 함수는 입력받은 input(x)에서 kernel_size(k)개씩 확인해 kernel_size 내에서 가장 큰 값을 출력합니다. maxout은 직선들 중 가장 큰 값을 취하므로 max_pool1d 함수를 이용해 직선 값들 중 가장 큰 값을 가져올 수 있습니다.

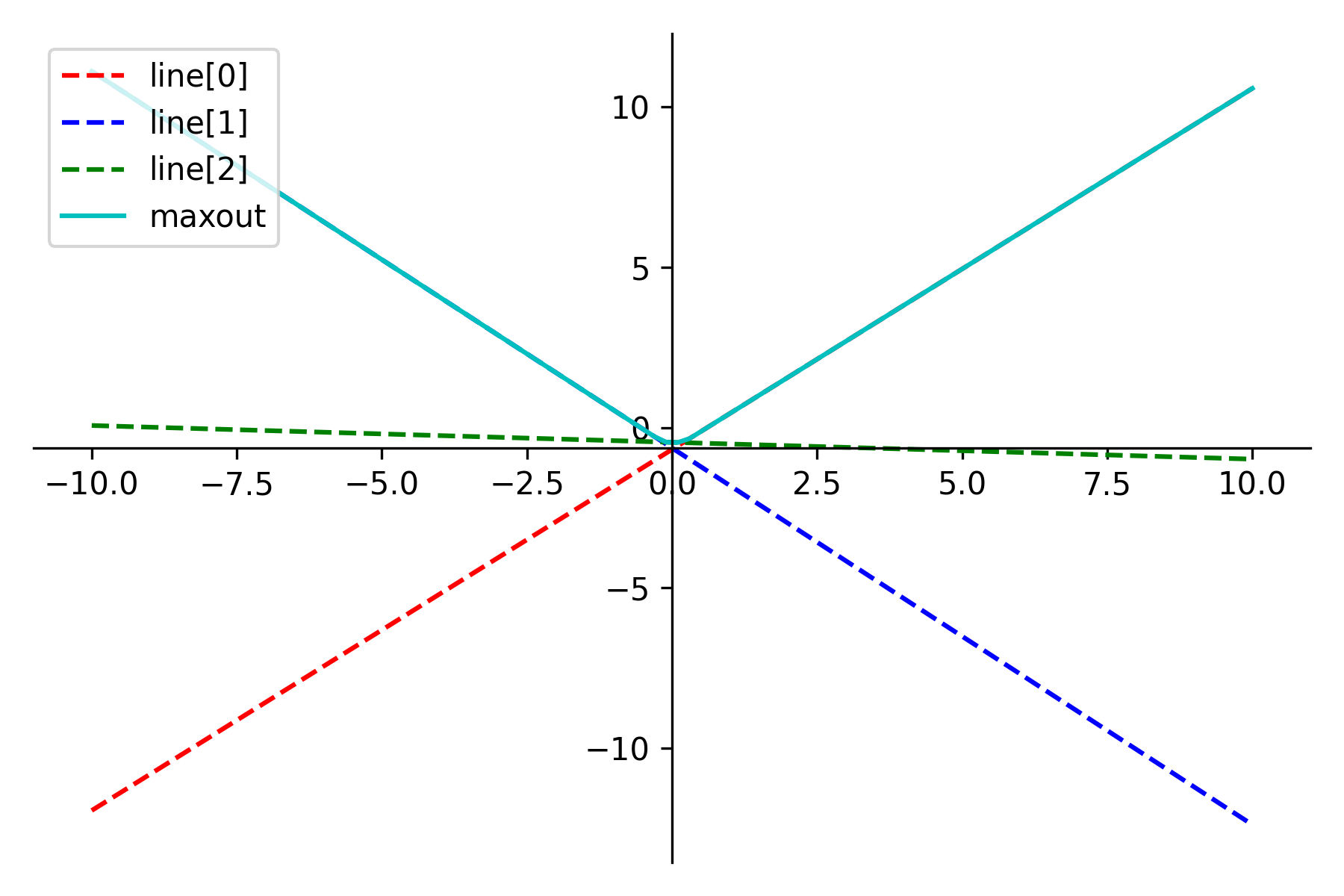
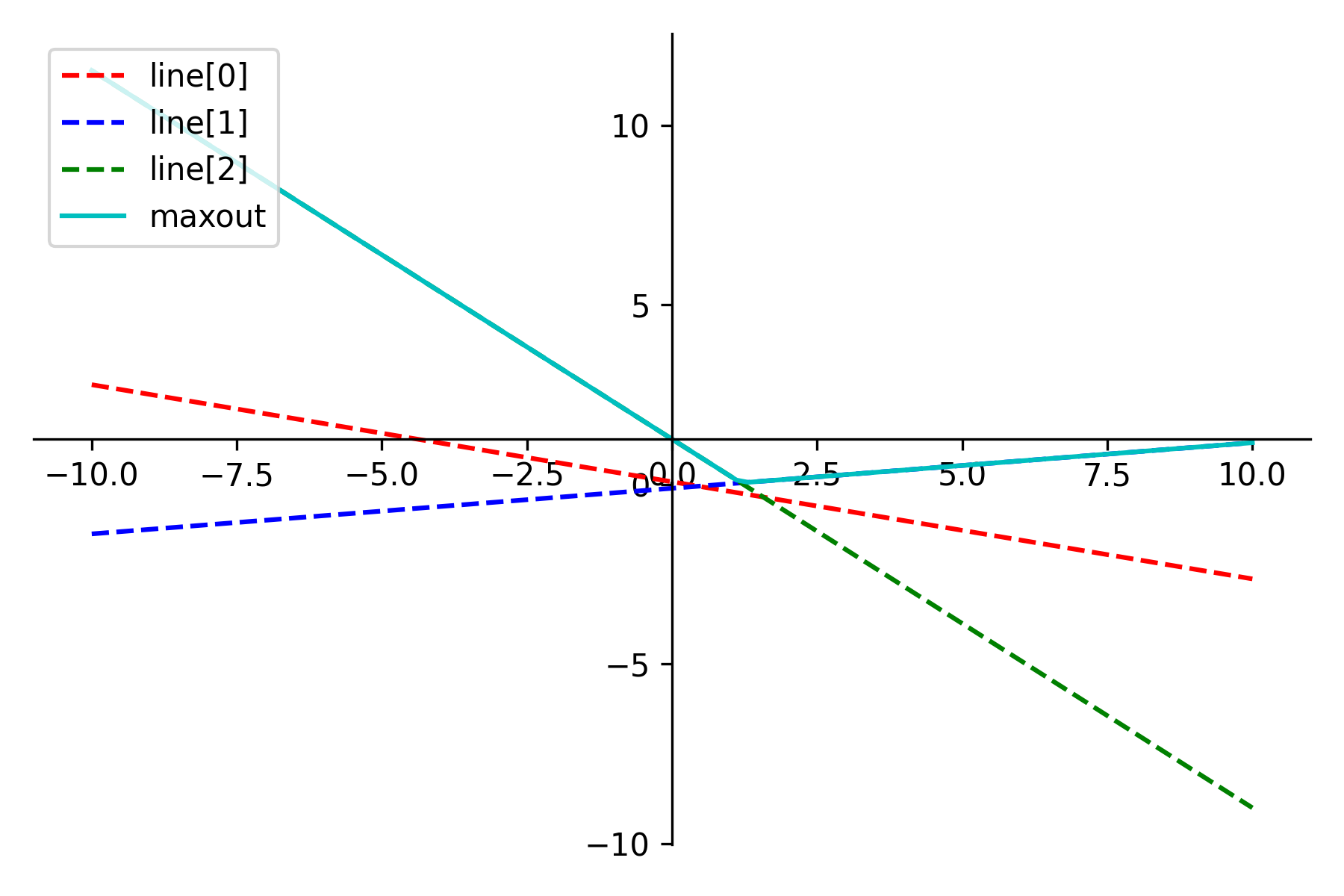
위 사진들은 모델을 학습하며 출력해본 maxout의 모양들입니다. 저는 $k=3$으로 설정해 학습을 했는데 maxout 논문의 Absolute value 예시와 비슷한 모양을 한 경우가 많았습니다. $k$ 값에 따라 학습의 효과가 증가하나 그만큼 cost 또한 높아지니 $k$ 값 조절이 필요한 것 같습니다.

구현한 maxout은 nn.Module을 상속해 custom layer로 사용할 수 있게 되어 nn.Sequential에 넣을 수 있게되었습니다.
discriminator는 maxout과 dropout을 사용하고 마지막 layer은 sigmoid로 0과 1 사이의 값을 출력할 수 있도록 했습니다.

class Discriminator(nn.Module):
  def __init__(self, img_shape=28*28):
    super(Discriminator, self).__init__()

    self.model = nn.Sequential(
        nn.Linear(img_shape, 512),
        Maxout(),
        nn.Dropout(0.5),
        nn.Linear(512, 256),
        Maxout(),
        nn.Linear(256, 1),
        nn.Sigmoid()
    )

  def forward(self, img):
    output = self.model(img)
    return output

3. 추가 설정 및 학습

3.1. 추가 설정

가장 중요한 모델 구현이 끝이 났습니다! 이제 loss, optimizer를 설정해야합니다.
loss는 BCELoss를 사용했습니다.

loss = nn.BCELoss().cuda()

$BCE(x, y) = - \frac{1}{N} \sum\limits_{i=1}^N y_i \cdot log(x_i) + (1-y_i) \cdot log(1-x_i)$ $\underset{G}{min} \underset{D}{max} V(D,G) = \mathbb{E} _{x \sim p _{data}}[logD(x)] + \mathbb{E} _{z \sim p_z(z)}[log(1-D(G(z)))]$

BCE loss의 구조가 익숙한 구조를 가지고 있지 않나요? GAN 논문에서 보았던 $V(D, G)$와 같은 구조임을 볼 수 있습니다.

BCE loss의 식에서 $y$가 정답 라벨, $x$가 $D$의 출력 값이라 생각하면 $V(D, G)$와 같은 방법으로 해석할 수 있습니다.
만약 $y=0$인 $G$가 생성한 이미지가 들어온다면 $y_i \cdot log(x_i)$ 부분은 $y_i=0$이므로 삭제되며 $log(1-x_i)$만 남게되며 이 값을 최대화해야 하기 때문에 $D$는 $x_i$를 최소화하기 위해 $D$의 결과 값인 $x_i$는 0에 가까운 값이 나와야 합니다.
반대로 $y=1$인 학습 데이터의 이미지가 들어온다면 $(1-y_i) \cdot log(1-x_i)$ 부분은 삭제되며 $log(x_i)$만 남게되며 이 값을 최대화해야 하기 떄문에 $D$는 $x_i$를 최대화해야 하기 위해 1에 가까운 값이 나와야 합니다.

optimizer는 기본 SGD를 사용했습니다. 논문에서는 momentum을 사용했다 언급되어 있어 momentum 값을 0.9로 넣어주었습니다.

optimizer_G = torch.optim.SGD(generator.parameters(), lr=learning_rate, momentum=0.9)
optimizer_D = torch.optim.SGD(discriminator.parameters(), lr=learning_rate,  momentum=0.9)

추가로 고정된 가우시안 노이즈 값인 sample를 설정했습니다. sample 값은 한 epoch마다 generator가 학습한 후 generator에게 입력해 generator가 생성하는 결과 이미지 히스토리를 보기 위함입니다.

sample = torch.zeros(batch_size, z_dim)
sample += (0.1**0.5)*torch.randn(batch_size, z_dim)
sample = sample.cuda()

3.2. 학습 결과

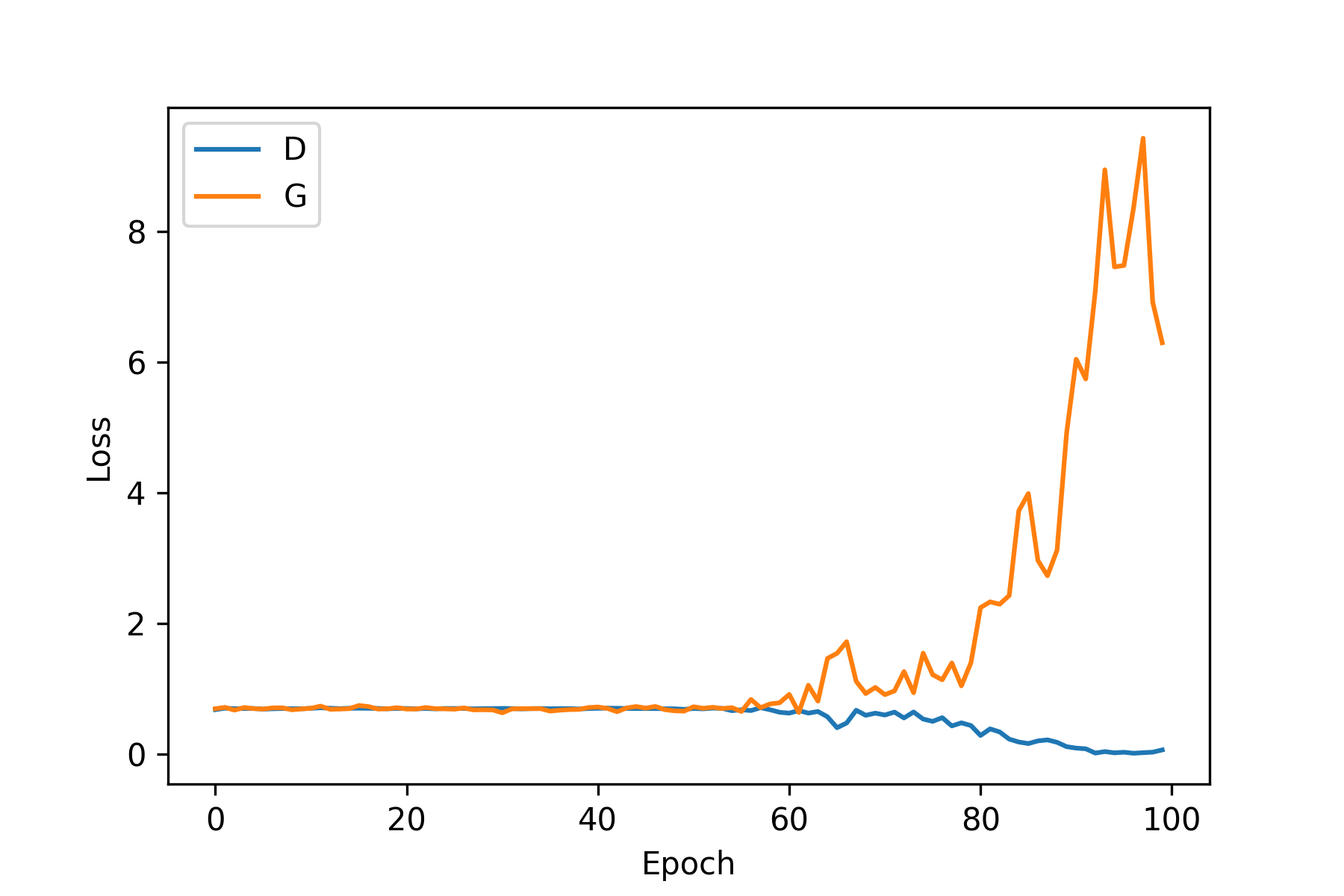
왼쪽은 $D$와 $G$의 loss를 나타낸 학습 그래프이고 오른쪽은 위에서 언급된 sample 노이즈 값을 1 epoch 학습이 끝날 때마다 $G$에 입력으로 넣었을 때 $G$의 결과 값을 나타낸 이미지를 모아놓은 히스토리입니다.

epoch 50 이전까지는 서로 비등비등한 loss 값을 나타내며 학습을 하다 갑자기 discriminator의 학습이 generator에 비해 월등히 좋아지며 generator의 loss 값이 상승하게 되고 학습이 정상적이지 않았음을 학습 그래프를 통해 볼 수 있습니다. 오른쪽의 생성 결과 히스토리 또한 비슷한 시기부터 점점 망가져 가는 모습이 보이네요.

하지만 한번에 좋은 결과가 나오는 걸 기대하면 안된다는 걸 모두가 알고 있죠ㅎ-ㅎ… 최적화 단계를 통해 더 좋은 결과를 기대해봅시다!

4. 최적화

gan의 경우 학습이 불안정해 더 나은 학습 방법을 찾는 연구자들이 많았습니다. ganhacks는 여러 학습 방법들이 나와있어 이 중 몇가지를 참고했습니다. 여러 기법들이 소개되어 있으니 코드 구현 중인 분들은 참고하시면 많은 도움이 될 것 같아요:)

4.1. Adam, lr

가장 처음 시도한 것은 optimizer 변형입니다.
ganhacks의 9: Use the ADAM Optimizer에 나와있는 방법입니다. 사실 가장 시도하기 좋은 방법으로 널리 알려져 있기도 한 Adam 사용입니다ㅎ
discriminator에는 SGD, generator에는 Adam을 사용하는 것이 추천되어 있어 $G$의 optimizer를 Adam으로 변경했습니다. 또한 learning_rate 값이 기존에는 0.01로 설정되어 있던 learning_rate 값을 0.0002까지 낮추어보았습니다.

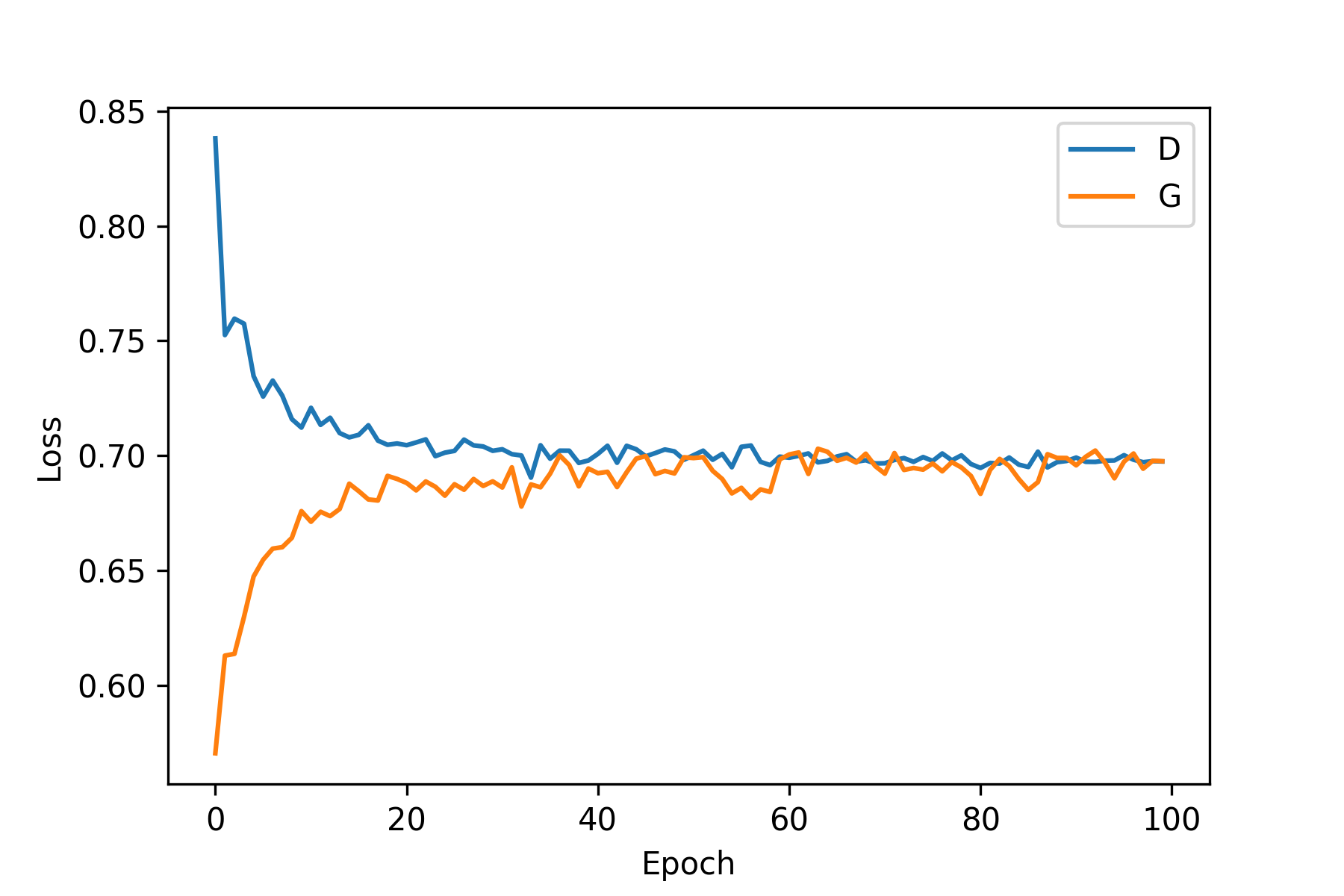
이전 학습 그래프에서 보이던 $D$가 $G$를 이겨버리는 모습은 보이지 않지만 결과 히스토리 이미지가 좋은 모습을 보이지도 않아버렸습니다.

$G$와 $D$가 균형이 맞아가며 같이 성장하는 모습이 가장 이상적이지만 이번 $D$와 $G$는 함께 성장하지 않기로 마음을 먹은 듯한 모습입니다… 더 좋은 방법을 찾아야 됨을 느꼈습니다.

4.2. norm, label

추가로 batchnorm과 soft label 방법을 추가로 테스트해보았습니다.

generator의 경우 학습을 할 때마다 결과 이미지들의 차이가 굉장히 심했고 학습이 불안정함을 알게 되었습니다. 학습의 안정성을 높이기 위해 batch normalization을 추가했습니다.

class Generator(nn.Module):
  def __init__(self, z_dim=100, img_shape=(28,28)):
    super(Generator, self).__init__()

    self.z_dim = z_dim
    self.img_shape=img_shape

    self.model = nn.Sequential(
        nn.Linear(self.z_dim, 256),
        nn.BatchNorm1d(256),
        nn.ReLU(),
        nn.Linear(256, 512),
        nn.BatchNorm1d(512),
        nn.ReLU(),
        nn.Linear(512, 784),
        nn.Sigmoid()
    )

  def forward(self, z):
      img = self.model(z)
      img = img.view(img.size(0), *self.img_shape)
      return img

그리고 ganhacks의 6: Use Soft and Noisy Labels에 나와있는 soft and loisy labels 방법을 사용해보았습니다.
참고 논문으로 나와있는 것은 Improved Techniques for Training GANs로 Ian Goodfellow도 저자로 등록되어 있는 OpenAI의 논문입니다.

적용 방법은 논문의 3.4 One-sided label smoothing에 나와있는데 학습 데이터에는 1, 생성 데이터에는 0의 값으로 discriminator를 학습시키는 것에 변형을 주어 학습 데이터에는 [0.9, 1] 사이의 값과 같이 smooth한 값을 넣는 것으로 더 좋은 결과를 유도할 수 있다고 합니다.

ones = ((torch.rand(batch_size, 1) * 0.1) + 0.9).cuda()
ones.requires_grad = False
zeros = torch.zeros(batch_size, 1).cuda()
zeros.requires_grad = False

$D$ 학습 시 loss 계산에 쓰이는 변수를 추가로 저장해 사용했습니다. 기존에는 torch.ones를 사용해 1의 값을 넣어주었지만 현재는 torch.rand를 사용해 [0.9, 1] 사이의 smooth한 값을 넣어주었습니다.

5. 최종결과

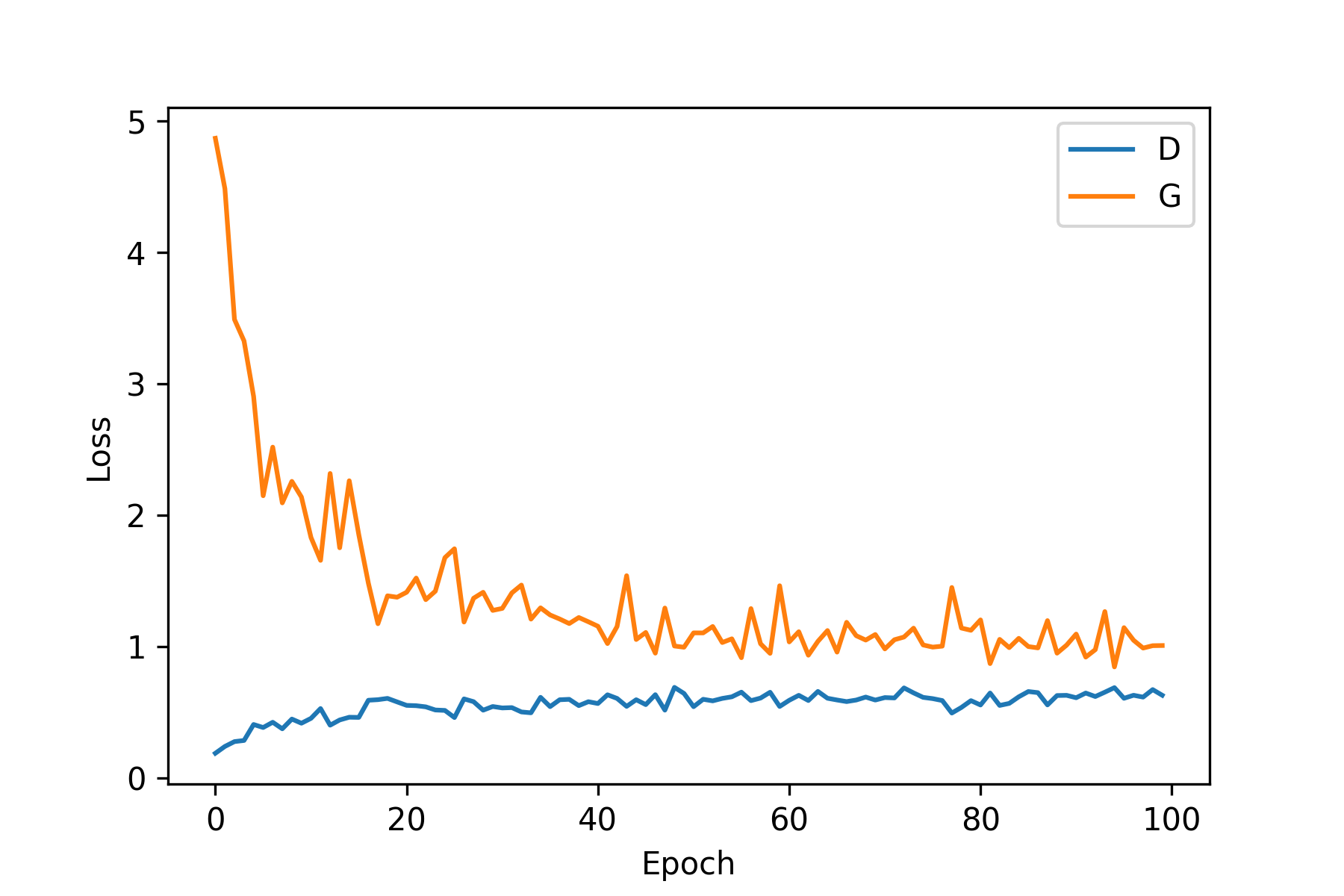
왼쪽은 학습 그래프, 오른쪽은 고정된 sample 노이즈의 히스토리 결과 이미지들입니다.
이전 결과에 비하면 확연하게 달라진 모습을 볼 수 있었습니다:)
학습 그래프에서는 $G$가 점점 안정되는 모습을 볼 수 있고 히스토리 결과에서도 9나 7과 비슷한 숫자들이 생성되는 것 볼 수 있습니다ㅎ-ㅎ
학습 그래프 모양을 봤을 때 아마 epoch을 더 크게 잡아 오래 학습을 시킨다면 더 좋은 결과를 얻을 수 있을 것 같다는 생각도 드네요.

만들어진 generator에 랜덤한 노이즈를 만들어 입력으로 주어 100개의 생성 이미지를 얻어 다음과 같은 결과를 얻을 수 있었습니다.

다행히 helvetica scenario처럼 같은 숫자들만 생성하는 것이 아닌 1~9까지 다양한 숫자들이 결과로 나오는 것을 확인할 수 있었습니다!

최종 코드는 github에서 확인하실 수 있습니다.

논문 구현 글은 여기서 끝입니다!
…
하지만 조금 여담을 해볼까합니다ㅎㅎ

위에 올린 ganhacks에도 나와있듯이 본문 코드에서 더 성능을 높이는 방법을 많습니다.
relu, maxout 사용이 아닌 leakyrelu를 사용하는 것과 generator의 마지막 layer로 sigmoid가 아닌 tanh를 사용하는 등 모델에 관련된 방법이 많았습니다. 하지만 논문 구현이 목표인만큼 논문에서 언급된 방법들은 최대한 유지하는 것이 맞다고 생각해서 바꾸지 않은 부분들이 있었습니다.
만약 gan 구현을 하고자 하시는 분들은 이 점 참고해서 더 좋은 방법들로 구현하시는 걸 추천드립니다ㅎㅎ