GAN?

GAN의 시작입니다! 너무나도 유명한 모델이고 빠르게 발전하고 있는 GAN 모델들의 초석이 된 논문인 Generative Adversarial Networks 논문을 정리해보고자 합니다. 논문 이해 위주의 글이며 Related Work 부분은 제외했습니다.

논문의 내용을 번역하고 개념이 부족할 수 있는 단어나 수식을 추가 설명하는 식으로 정리해보았습니다. 추가되었으면 하는 부분이나 이해가 가지 않으시는 부분은 댓글로 남겨주시면 저도 아직 부족하지만 최대한 답을 해드릴 수 있도록 노력해보겠습니다. 잘못된 부분을 지적해 주시는 것도 언제나 환영합니다. 감사합니다:)

1. Introduction

지금까지의 딥러닝 모델들 중 가장 눈에 띄는 성공적인 모델은 다양한 입력을 클래스 라벨로 분류하는 고차원의 판별 모델(discriminative model)과 관련되어 있다. 이러한 놀라운 성공은 gradient 학습에 특히 잘 작동하는 piecewise linear units를 사용하여 주로 dropout과 역전파 알고리즘을 기반으로 한다. 심층 생성 모델(Deep generative model)은 최대 우도 측정(maximum likelihood estimation)을 사용하는데 여기서 발생하는 확률론적 계산을 근사화하는 것이 어렵고 PLU의 장점을 결과를 생성할 때 활용하기 어렵기 때문에 눈에 띄지 않는 모델이였다. 우리는 이러한 어려움을 회피하는 새로운 생성 모델 추정 절차를 제안한다.

PLU(piecewise linear units) 범위 별로 나뉘어진(piecewise) 직선 함수가(linear) activation 함수로 쓰이는 경우 이 함수를 piecewise linear units라 합니다.
아래의 그림처럼 범위가 나뉘어져 $ x $ 값에 따라 적용되는 직선의 함수가 다른 경우 piecewise linear function라 하며 이 함수를 activation 함수로 사용한다면 piecewise linear unit을 사용했다 할 수 있습니다.


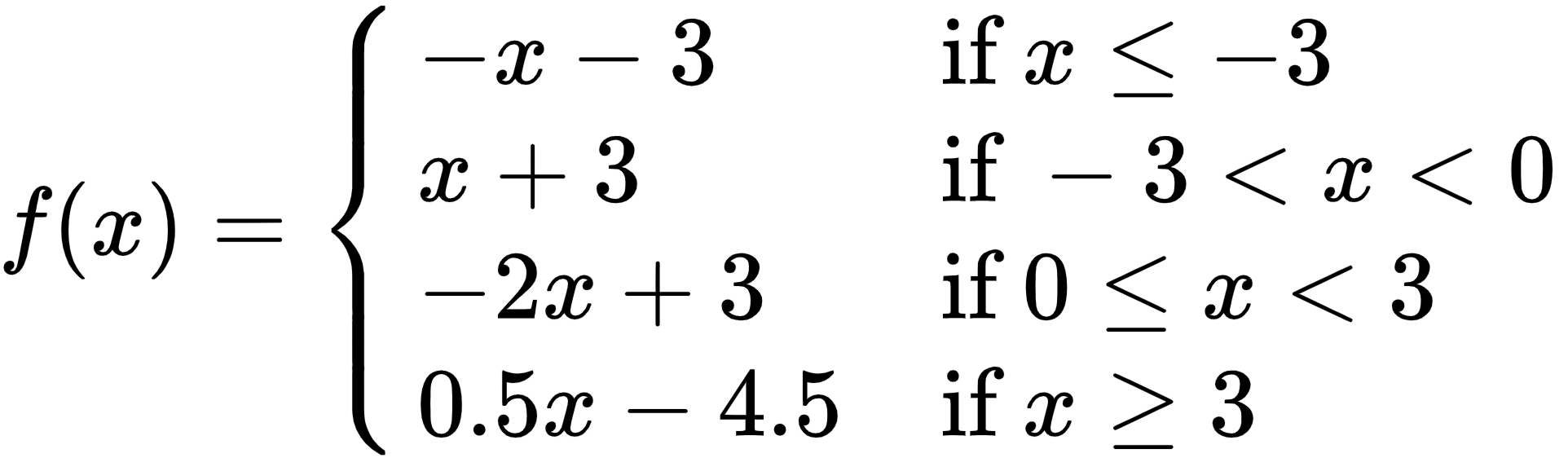
최대 우도 측정(MLE / maximum likelihood estimation) likelihood는 가능도/우도란 말로도 사용되며 조건부 확률 $p(z|x)$로 이해할 수 있는데 어떤 모델 x에서 관측값 z가 나올 확률입니다.
여기서 maximum을 추가한 maximum likelihood는 likelihood 함수의 최대값을 찾는 방법으로 사건이 일어날 가능성을 가장 크게 만들기 위한 데이터 분포/모델의 파라미터를 찾는 방법입니다.
아래 참고에 표시된 StatQuest의 영상이 이해하기 쉽게 설명되어 있다 생각합니다. 추천드립니다:)

참고
- 다크 프로그래머님의 베이즈 정리, ML과 MAP, 그리고 영상처리
- StatQuest With Josh Starmer님의 Maximum Likelihood 최대 우도 추정



제안하는 적대적 네트워크 프레임워크에서 생성모델은 판별모델과 대립된다. 결과 이미지가 생성 모델 분포에서 왔는지 학습 데이터 분포에서 왔는지를 결정하는 것을 판별 모델이 학습한다. 생성 모델을 위조 지폐를 제작해 적발 없이 사용하려는 위조 지폐 팀과 유사하다고 생각할 수 있고 판별 모델은 위조 지폐를 적발하려는 경찰과 유사하다고 볼 수 있다. 이 게임의 경쟁은 위조품과 진짜 물건을 구분할 수 없을 때까지 두 팀 모두 방법을 개선하도록 만든다.

본 논문에서 생성 모델과 판별 모델은 다층 퍼셉트론으로 이루어져 있으며 이 특수한 케이스를 적대적 네트워크(Adversarial nets)라 부른다. 우리는 두 모델을 역전파, dropout 알고리즘을 사용하려 학습하고 순전파만을 사용하여 생성 모델에서 결과 이미지를 추출할 수 있다. approximate inference나 Markov chains은 필요하지 않다.

approximate inference(근사추론) 보통 inference는 모델의 학습이 끝난 후 모델에게 데이터를 입력해 결과를 추론하는 과정을 말하지만 approximate inference는 모델을 학습하는 과정에서 수행되는 inference 과정을 말합니다. 이때 approximate inference는 사후확률(posterior) 분포를 다루기 위해 사용되며 크게 Sampling Method와 Variational Method로 구분됩니다.

논문에서 approximate inference를 언급한 이유는 GAN 이전에 사용되던 모델인 VAE(Variational Auto-Encoder)를 포함해 bayesian inference에서 approximate inference 방법 중 하나인 variational inference(변분추론)를 사용하기 때문입니다. VAE에서는 decoder가 데이터의 사후확률을 학습하는데 사후확률은 계산이 복잡한 경우가 많아 이를 다루기 쉬운 분포 $q(z)$로 근사할 때 variational inference를 사용합니다.

참고
- Kim Hyungjun 님의 Approximate Inference란 무엇인가?
- ratsgo 님의 변분추론(Variational Inference)

Markov chains(마르코프 체인) 특정 상태의 확률이 오직 과거의 상태에 의존하는 성질을 Markov 성질이라 합니다. Markov chain이란 이런 Markov 설징을 가진 이산 확률 과정을 의미합니다. 이때 차수에 따라 의존하는 과거의 크기가 달라집니다.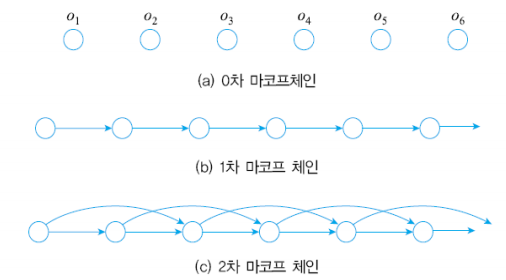 r=1이면 1차 마르코프 체인으로 t시점에서는 오직 t-1시점의 영향만 받습니다. r=2이면 2차 마르코프 체인으로 t시점에서는 오직 t-1, t-2시점의 영향만 받습니다.

마르코프 체인의 대표적인 예시로는 학생 때 어디선가 많이 본 듯한 문제인 비가 올 확률을 구하는 문제입니다. "비가 온 다음 날에 비가 올 확률은 70%이고 비가 오지 않은 다음 날에 비가 올 확률은 20%입니다" 라는 문장을 모델화 한다면 다음과 같은 그림이 나오게 됩니다. 이 문제의 경우 이전 날에 대한 영향만 받으니까 1차 마르코프 모델이 됩니다.


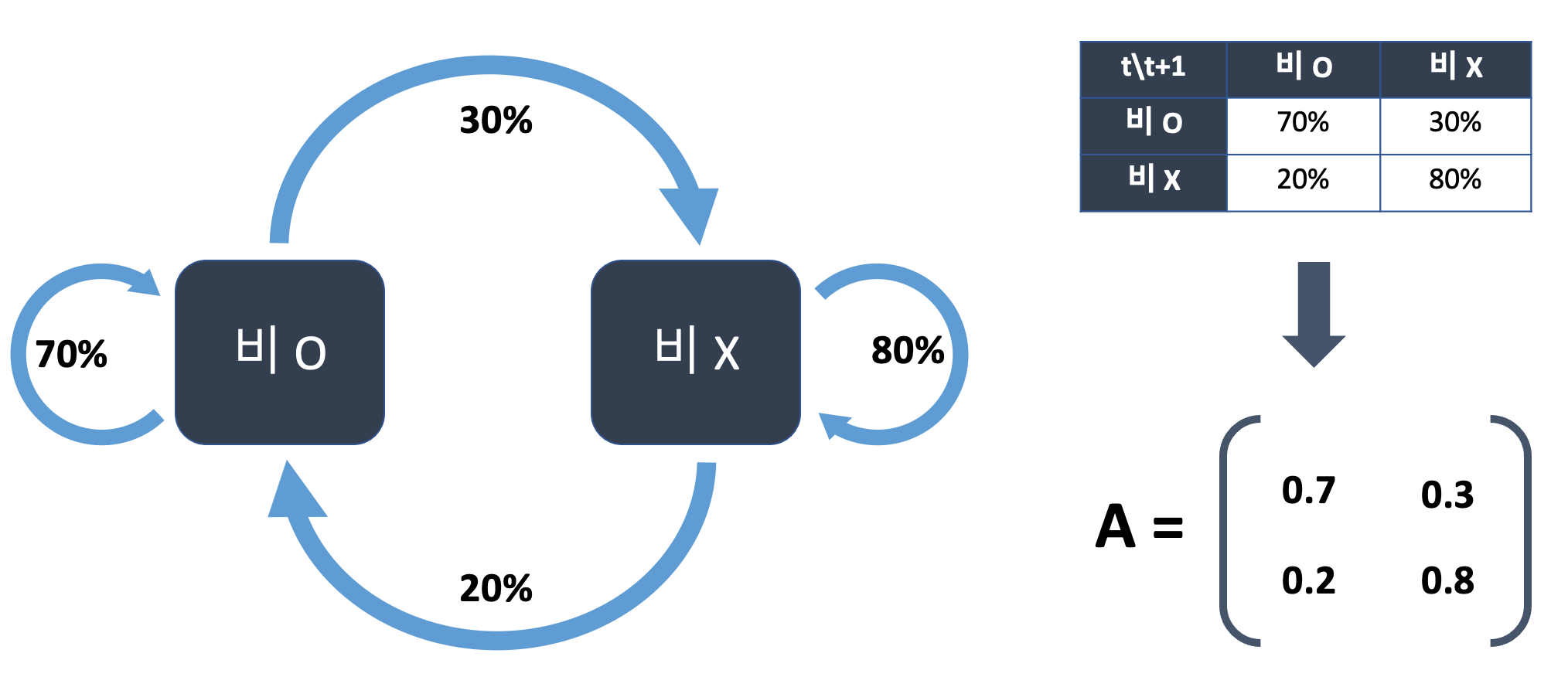
위와 같은 상태 전이도를 가지고 있을 때 전이 행렬은 P와 같으며 이런 전이 행렬을 가지고 계산하는 것이 Markov chain입니다. 예시로 오늘 비가 온 다음 날 비가 오지 않고 모레 비가 올 확률을 Markov chain을 이용한다면 다음과 같습니다.
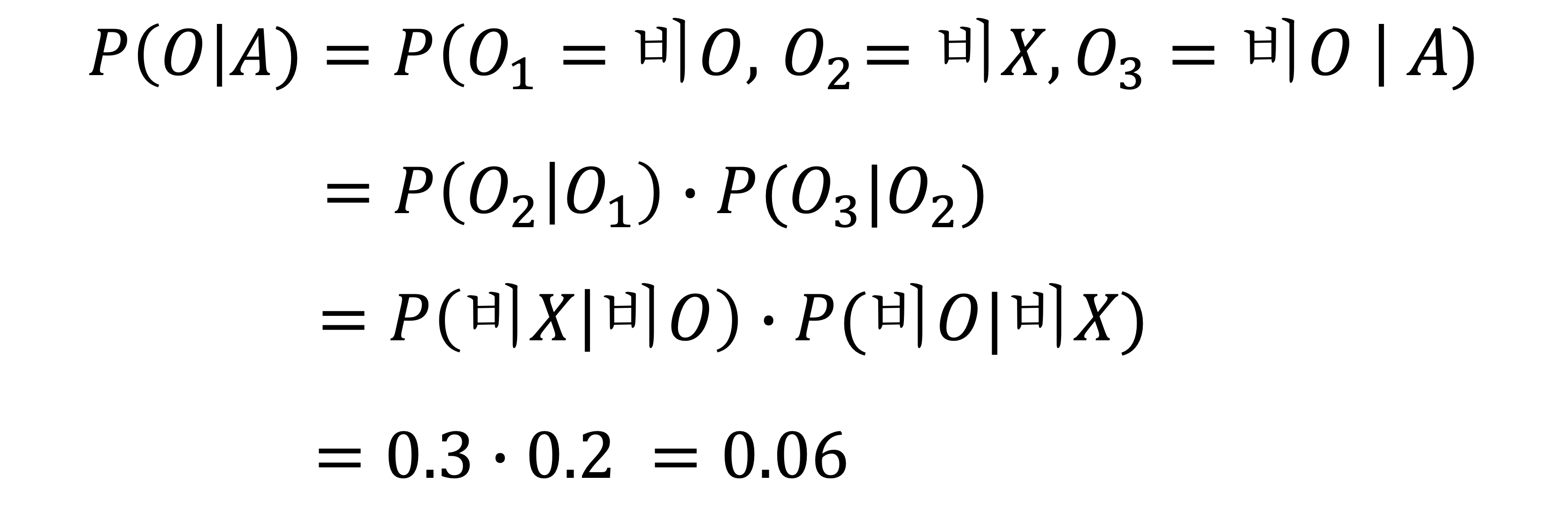
참고
- 티랩님의 HMM(Hidden Markov Model) 2. 마르코프 모델
- ratsgo님의 은닉마코프모델(Hidden Markov Models)

3. Adversarial nets

적대적 모델링 프레임워크는 모델이 둘 다 다층 퍼셉트론인 경우 가장 쉽게 적용할 수 있다. 데이터 $x$에 대한 생성 모델 분포인 $p_g$를 학습하기 위해서 우리는 우선적으로 입력 노이즈 변수 $p_z(z)$를 정의한 다음 $G$가 매개 변수 $\theta_g$를 가진 다층 퍼셉트론에 의해 표현되는 데이터 공간에 대한 매핑 $G(z;\theta_g)$을 표현한다. 또한 우리는 단일 스칼라를 출력하는 두번째 다층 퍼셉트론인 $D(x;\theta_d)$를 정의한다. $D(x)$는 $x$가 $p_g$가 아닌 데이터에서 나왔을 확률을 나타낸다. 우리는 $D$를 학습데이터와 $G$에서 생성된 결과 이미지 모두에 올바른 라벨 값을 할당할 확률을 최대화하도록 훈련한다. 우리는 동시에 $G$가 $log(1-D(G(z)))$를 최소화하도록 훈련한다.

\(\begin{align} \underset{G}{min} \underset{D}{max} V(D,G) = \mathbb{E} _{x \sim p _{data}}[logD(x)] + \mathbb{E} _{z \sim p_z(z)}[log(1-D(G(z)))] \tag{1} \end{align}\)

$\mathbb{E}$ 는 기댓값을 의미하며 변수의 평균값을 나타냅니다.
$\sim$은 통계량에서 변수가 특정 분포를 따르는 것을 나타낼 때 사용합니다. 여기서 $x \sim p_{data}$ 는 $x$ 가 $data(x)$ 분포,즉 학습 데이터 분포를 따르는 것을 의미합니다.
$\mathbb{E}_{z \sim p_z(z)}$는 노이즈 분포인 $p_z(z)$를 따르는 $z$의 기댓값을 의미합니다. 본 논문에서 노이즈 데이터로 어떤 것을 사용하는지는 언급되지 않지만 보통 가우시안 노이즈를 사용합니다.

$\underset{G}{min} \underset{D}{max}$의 의미는 $G$는 우측 수식의 최소화하도록, $D$는 우측 수식을 최대화하도록 학습함을 의미합니다. 수식에 대한 설명은 Algorithm 1에서 반복되어 나오므로 Algorithm1에서 자세하게 설명해드리겠습니다.


다음 절에서 우리는 $G$와 $D$가 충분한 학습을 한 경우 $G$가 데이터 생성 분포를 복구할 수 있음을 보여주는 적대적 네트워크 이론적 분석을 제시한다. 학습 중 $D$를 완벽하게 최적화하는 것은 금지되며 대신 우리는 $D$를 최적화하는 $k$ 단계와 $G$를 최적화하는 한 단계를 번갈아 진행한다. 이것은 $G$가 천천히 변화하는 동안 $D$가 최적의 결과 근처에 유지하는 결과를 가져온다. 이 전략은 학습의 일부로 Markov chain에서 burn-in 문제를 회피하기 위해 SML/PCD가 한 학습 단계에서 다음 학습 단계로 Markov chain의 샘플을 유지하는 방법과 유사하다. 이 절차는 Algorithm 1에 공식으로 제시되어 있다.

학습 중 $D$가 완벽하게 최적화하는 것을 금지한다는 말은 $D$의 성능이 $G$에 비해 월등히 좋아 $G$가 잘 학습되지 않는 것을 방지한다는 것을 의미합니다. 이를 위해 $D$를 학습하는 것과 $G$를 학습하는 것을 번갈아 시행하는데 이때 $D$를 몇 번 반복 학습할지는 $k$ 변수 값에 따라 달라집니다.

Markov burn-in Markov chain이 수렴하기까지 필요한 시행횟수를 Burn-in이라 부릅니다. Markov 초기값에 따라 Monte Carlo 분포에 수렴하기까지 초기 시행단계들을 의미하는데 MCMC(Markov chain Monte Carlo)에서는 이 기간을 burn-period라 부르며 이때 샘플링된 것들은 버려집니다.

대표적으로 RBM(Restricted Boltzmann Machine)에서 사용되며 RBM은 모델 분포의 기대값을 계산해야 하는데 variable space의 공간이 너무 커 적절한 샘플들을 구하는 것이 어렵고 시간이 많이 걸려 이를 해결하기 위해 MCMC를 활용합니다. MCMC에서는 각 단계별 초기화로 인한 markov burn-in 과정이 필요하고 이에 대한 cost가 큰 것이 문제가 됩니다.

SML/PCD SML(Stochastic Maximum Likelihood)/PCD(Persistent Contrastive Divergence)는 위에서 언급된 burn-in cost를 줄이기 위한 전략입니다.

Gibbs sampling을 실행하여 모델 입력 분포를 대표하는 샘플을 추출하고 분포의 기대값을 추정하는 CD(Contrastive Divergence) 알고리즘이 학습 데이터에 편중된 샘플 형태만을 추출해 모델 분포를 대표하기에 적절한 샘플을 얻는데 한계가 있어 PCD가 제안되었습니다.

PCD는 Gibss sampling을 수행하기 위해 초기 샘플을 학습 데이터가 아닌 이전의 갱신 과정에서 Gibbs sampling에 의해 추출된 샘플을 사용하여 모델 입력 분포에 더 적합한 샘플을 얻습니다. 이전에 수행된 Gibbs Sampling 결과를 다음 트레이닝 Markov Chain의 시작점으로 사용함으로써 burn-in 과정을 피할 수 있습니다.

- 참고 : Sargur N. Srihari 님의 Stochastic Maximum Likelihood and Contrastive Divergence


실제로 equation (1)은 $G$가 잘 학습할 수 있는 충분한 gradient를 제공하지 않을 수도 있다. 학습 초기에 G의 성능이 좋지 않을 때 $D$는 학습 데이터에서 온 샘플과 $G$에서 온 샘플이 분명하게 다르다는 것을 파악할 수 있어 높은 신뢰도를 가지며 $G$에서 온 샘플을 구별할 수 있다. 이 경우 $log(1-D(G(z)))$는 포화상태가 되어 굉장히 낮은 값을 가지게 된다. 우리는 $log(1-D(G(z)))$를 최소화하도록 $G$를 학습하는 것보다는 $D(G(z))$를 최대화하도록 $G$를 학습하는 것이 낫다. 이 목표 함수를 $G$와 $D$의 역학에서 동일한 고정점을 가져오지만 학습 초기에 훨씬 더 강력한 gradient를 제공한다.

기존의 식이 $log(1-D(G(z)))$를 최소화하는 것인데 초기에 $G$를 학습할 시 성능이 좋지 않을 테니 $D$는 $G$에서 생성된 데이터를 쉽게 구별할 수 있을 것입니다. 그렇다면 수식의 결과는 $log(1)$에 가까운 값이 나오는 데 문제는 이때의 gradient 값이 완만해 학습의 속도가 굉장히 낮아집니다.
이를 해결하기 위해 수식을 $-log(D(G(z)))$를 최대화하는 방법으로 $G$를 학습하며 이 경우 초기 gradient 값이 가파르게 되어 학습이 빠르게 진행됩니다.


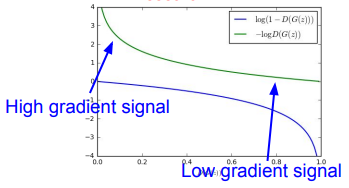
위 그림에서 학습 초기(x축 우측)의 파란선의 $log(1-D(G(z)))$의 경우 gradient가 낮고 초록선의 $-log(D(G(z)))$의 경우 gradient가 가파른 것을 볼 수 있습니다. 따라서 초기 $G$의 학습 속도를 위해 $log(1-D(G(z)))$가 아닌 $-log(D(G(z)))$를 사용합니다.


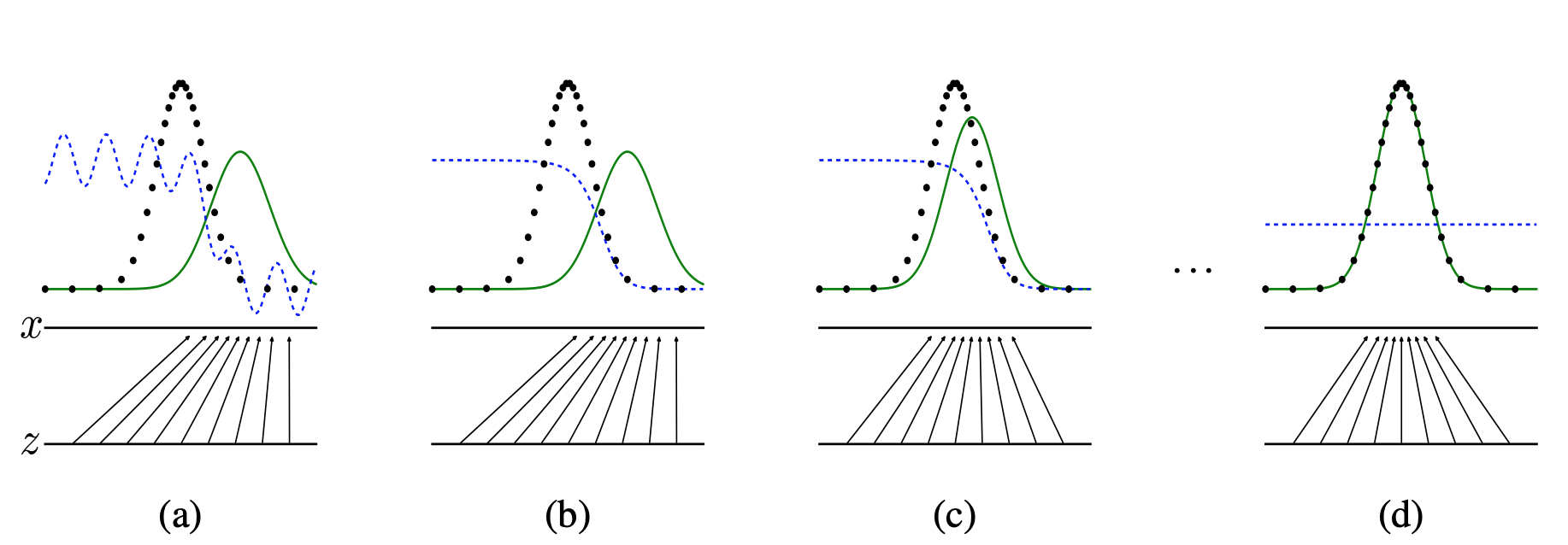figure1 Figure 1. 적대적 생성 신경망은 데이터 분포 $p_x$(검은색 점선) 의 샘플과 생성 분포 $p_g(G)$(녹색 실선) 의 샘플을 구별하도록 판별 분포($D$, 파란색 점선) 를 동시에 업데이트하며 학습된다. 아래의 수평선은 $z$가 샘플링되는 영역이며 균일하게 분포된다. 위의 수평선은 $x$ 영역의 일부이다. 위쪽으로 향하는 화살표는 비균등 분포 $p_g$가 $x=G(z)$로 대응되도록 변환된 샘플이 되는 방법을 보여준다. $G$는 $p_g$의 밀도가 $p_x$ 보다 높은 영역에서 수축하고 $p_g$ 의 밀도가 $p_x$ 보다 낮은 영역에서 팽창한다.

(a) $p_g$ 는 $p_{data}$와 어느정도 유사성을 보여주며 $D$는 부분적으로 구별할 수 있다.
(b)알고리즘 내부에서 $D$는 학습 데이터에서 온 샘플을 구별할 수 있도록 학습되어 $D^*(x) = \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$ 에 수렴한다.
(c)$G$를 업데이트한 후, $G$는 $D$가 $G(z)$가 데이터로 분류될 가능성이 더 높은 영역으로 흐르도록 유도했다.
(d)여러 단계의 학습을 거쳐 $G$와 $D$가 충분학 학습을 했다면 $p_g=p_{data}$이기 때문에 둘 다 개선할 수 없는 지점에 도달하게 된다. 판별 모델은 두 분포를 구분할 수 없게 된다. 즉 $D(x)=\frac{1}{2}$이다.

$p_x$ : 실제 데이터 분포(학습 데이터)
$p_g(G)$ : 생성 모델에서 만들어진 데이터 분포(생성 데이터)
$z$ : 생성 모델의 입력값이 되는 값(노이즈 데이터)
$x$ : 실제 데이터(학습 데이터)

(a)는 초기 단계로 $D$인 파란선이 $G$의 분포인 초록선이 있는 부분에서는 $G$에서 만든 데이터라 판단해 상대적으로 낮은 값을 출력하지만 불안정한 모습인걸 볼 수 있습니다.

(b)에서는 $D$의 학습 단계를 거친 모습입니다. (a)에 비하면 안정된 상태를 보여주지만 k step 만큼만 학습한 $D$의 상태로 아직 완벽하게 학습 데이터와 $G$의 데이터를 구별하진 않습니다.

(c)에서는 $G$의 학습 단계를 거친 모습입니다. (b)에 비하면 학습 데이터 분포인 검은 점선과 $G$의 분포인 초록선이 이전보다 유사한 모양을 띈 것을 확인할 수 있습니다.

(d)는 (b)와 (c) 단계를 여러번 반복해 가장 이상적인 $G$의 상태에 도달한 모습입니다. $G$의 분포는 학습 데이터의 분포와 완전히 같으며 $D$는 어떤 데이터를 주어도 구별하지 못해 $D(x) = \frac{1}{2}$ 에 수렴하게 됩니다.

4. Theorical Results

Algorithm 1 적대적 생성 네트워크의 Minibatch Stochastic gradient 학습. 판별 모델에 적용할 단계 수인 k는 hyper parameter이다. 실험에서는 가장 작은 코스트 값인 $k=1$ 을 사용했다.

for iteration의 수 do
    for k 단계의 수 do
       $-$ $p_g(z)$에서 얻은 m개의 샘플 {$z^{(1)}, …, z^{(m)}$}
      $\rightarrow$ $G$가 $z$를 입력받아 생성한 데이터로 이루어진 minibatch
       $-$ $p_{data}(x)$를 생성하는 데이터에서 얻은 m개의 샘플 {$x^{(1)}, …, x^{(m)}$}
       $\rightarrow$ 학습 데이터 $x$에서 얻은 데이터로 이루어진 minibatch
       $-$ stochastic gradient를 이용해 아래 수식을 최대화하도록 판별 모델을 업데이트

\[\bigtriangledown_{\theta_d} \frac {1}{m} \sum\limits_{i=1}^m[logD(x^{(i)})+log(1-D(G(z^{(i)})))]\]

$\bigtriangledown$은 gradient를 의미하고 $\theta$는 모델의 파라미터(가중치)를 의미합니다.
따라서 $\bigtriangledown_{\theta_d}$는 판별 모델의 gradient를 수식에 따라 최대화/최소화하도록 모델의 가중치를 업데이트한다는 것을 의미합니다.

수식은 2개의 로그 함수로 이루어져 있으며 수식 값을 최대화하기 위해서는 2개의 값 모두를 최대화해야 합니다.
첫번째 로그 함수인 $logD(x^{(i)})$는 $D(x^{(i)})$값이 1이 될 때 최대가 됩니다. 따라서 판별 모델($D$)이 학습 데이터인 $x^{(i)}$을 입력받을 경우 학습 데이터에서 온 값이라 판단해 1을 출력해야 합니다.

두번째 로그 함수인 $log(1-D(G(z^{(i)})))$ 를 최대화하기 위해서는 $1-D(G(z^{(i)}))$를 최대화해야 하며 판별 모델의 결과인 $D(G(z^{(i)}))$ 값이 0이 될 때 최대가 됩니다. 따라서 판별 모델이 생성 테이터인 $G(z^{(i)})$를 입력받을 경우 생성 모델($G$)이 만든 생성 데이터라 판단해 $D(G(z^{(i)}))$ 값이 0이라 판단해야 합니다.

수식으로 나와 복잡해보이지만 수식을 해석해보면 결국 판별 모델이 학습 데이터를 입력으로 받은 경우는 이 데이터는 학습 데이터라 판단해 1을 출력하고 생성 모델로부터 생성된 데이터를 받은 경우는 생성 데이터라 판단해 0을 출력하도록 판별 모델을 학습한다는 것을 의미합니다.

    end for
    $-$ $p_g(z)$에서 얻은 m개의 샘플 {$z^{(1)}, …, z^{(m)}$} 로 이루어진 minibatch
    $-$ stochastic gradient를 이용해 아래 수식을 최소화하도록 생성 모델을 업데이트

\[\bigtriangledown_{\theta_d} \frac {1}{m} \sum\limits_{i=1}^mlog(1-D(G(z^{(i)})))\]

수식 값을 최소화하기 위해서는 $1-D(G(z^{(i)}))$가 최소화되어야하므로 $D(G(z^{(i)}))$ 값을 최대화해야 합니다.
$D(G(z^{(i)}))$의 최대화 값은 1, 즉 판별 모델이 생성 모델이 만든 $G(z^{(i)})$를 생성 모델이 생성한 값이 아닌 학습 데이터 온 값이라 판별하도록 생성 모델을 학습합니다.

end for
gradient 기반 업데이트는 모든 표준 gradient 기반 학습 규칙을 사용할 수 있으며 우리는 실험에 momentum을 사용했다.

4.1 Global Optimality of $p_g=p_{data}$

Proposition 1. $G$가 고정된 상태에서 최적의 판별 모델 $D$는 다음과 같다.

\[D^*_G(x) = \frac{p _{data}(x)}{p _{data}(x)+p_g(x)} \tag{2}\]

$p_{data}(x)$는 학습 데이터 분포, $p_g(x)$는 생성 모델이 생성한 데이터 분포입니다.
최적의 판별 모델은 두 분포를 구별할 수 있어 학습 데이터와 생성 모델 데이터를 입력으로 주었을 때(분모) 학습 데이터(분자)만 구별할 수 있음을 의미합니다.


proof. 어떤 생성 모델 $G$가 주어졌을 때 판별 모델 $D$에 대한 학습 기준은 $V(G, D)$ 값을 최대화 하는 것이다.

\(\begin{align} V(G, D) &= \mathbb{E}_ {x \sim p_ {data}}[logD(x)] + \mathbb{E}_ {z \sim p _ z(z)}[log(1-D(G(z)))] \\ &= \int_xp_{data}(x)log(D(x))dx + \int_zp_z(z)log(1-D(g(z)))dz \\ &=\int_xp_{data}(x)log(D(x)) + p_g(x)log(1-D(x))dx \tag{3} \end{align}\)

3절의 Adversarial 에서 나왔던 식인 첫 줄에서 식을 유도할 수 있습니다.

$\mathbb{E}$는 기댓값을 의미하고 학습 데이터는 연속확률변수(주사위처럼 정해진 값만 나오는 것이 아닌 실수 범위 내에 무한한 확률 변수)이므로 연속확률변수의 기댓값을 구하는 공식으로 $E[X] = \int ^\infty _{-\infty} xp(x)dx$를 적용할 수 있습니다.
기댓값 공식인 $E[X] = \int ^\infty _{-\infty} xp(x)dx$ 을 적용해 첫번째 줄의 식이 두번째 줄의 식으로 변형됩니다.

두번째 줄의 $g(z)$는 생성 모델이 노이즈 데이터를 입력받아 생성한 데이터를 의미하므로 생성 모델이 데이터 $x$를 생성했다 할 수 있어 생성 모델이 도메인 $z$를 도메인 $x$로 변형하면 세번째 줄의 식이 완성됩니다.



임의의 $(a, b) \in \mathbb{R}^2 / {0, 0}$ 에 대하여 함수 $y \rightarrow alog(y) + blog(1-y)$는 $\frac{a}{a+b}$일 때 $[0, 1]$ 범위 안에서 최대값을 달성한다.

세번째 줄의 식에서 $p_ {data}(x)$를 $a$로, $p_g(x)$를 $b$로 치환하고 $D(x)$를 $y$로 치환한다면 $\int_xp_{data}(x)log(D(x)) + p_g(x)log(1-D(x))dx \to alog(y)+blog(1-y)$로 식이 변형됩니다.

이 식을 $y$에 대해 미분한다면 $\frac{a}{y}-\frac{b}{1-y}$가 됩니다. 극값이기 위해서는 도함수 값이 0이므로 $\frac{a}{y}-\frac{b}{1-y} = 0 \rightarrow a-ay = by \rightarrow (a+b)y = a \rightarrow y = \frac{a}{a+b}$로 $\frac{a}{a+b}$일 때 최대값을 달성함을 증명할 수 있습니다.
$alog(y)+blog(1-y)$ 그래프로 표현한 것으로 $a$와 $b$값을 1로 고정해두긴 했지만 $[0, 1]$ 범위 사이에서 극값을 가짐을 확인할 수 있습니다.



$D$에 대한 훈련 목표는 조건부 확률 $P(Y= y|x)$를 추청하기 위한 log-likelihood를 최대화한 것으로 해석될 수 있으며, 여기서 $Y$는 $x$가 $p_{data}(y=1)$ 또는 $p_g(y=0)$에서 왔는지에 대한 여부를 나타낸다. Eq 1. 식을 다음과 같이 재구성할 수 있다.

\(\begin{align} C(G) &= \max\limits_{D}V(G,D) \\ &= \mathbb{E}_ {x \sim p_ {data}}[logD^*_ G(x)] + \mathbb{E} _{z \sim p_z}[log(1-D^ *_G(x))] \\ &= \mathbb{E} _{x \sim p _{data}}[log \frac{p _{data}(x)}{p _{data}(x) + p_g(x)}] + \mathbb{E} _{z \sim p_z}[log \frac{p_g(x)}{p _{data}(x)+p_g(x)}] \tag{4} \end{align}\)

Eq1.은 $\underset{G}{min} \underset{D}{max} V(D,G) = \mathbb{E} _{x \sim p _{data}}[logD(x)] + \mathbb{E} _{z \sim p_z(z)}[log(1-D(G(z)))]$ 입니다.
저희는 $G$가 고정된 상태에서 최적의 $D$를 증명하는 중이니 식에서 $G$부분을 고정한다면 위 식의 두번째 줄로 변형됩니다.

두번째 줄의 식에서 증명한 Proposition 1인 $D^*_G(x) = \frac{p _{data}(x)}{p _{data}(x) + p_g(x)}$ 를 대입하면 세번째 줄로 식이 변형됩니다.



Theorem 1. 가상 훈련 기준 $C(G)$의 전역 최소값은 $p_g = p_ {data}$인 경우에만 달성된다. 이때 $C(G)$는 $-log4$ 값을 달성한다.

proof. $p_g = p_ {data}$인 경우, $D^* _G(x) = \frac{1}{2}$이다.(Eq. 2를 고려) 따라서 Eq. 4에서 $D^*_G(x) = \frac{1}{2}$를 적용하면 우리는 $C(G) = log \frac{1}{2} + log\frac{1}{2} = -log4$임을 찾을 수 있다. 이것이 $p_g=p _{data}$에 대해서 도달하는 $C(G)$의 최댓값임을 확인하려면 다음을 확인해야 한다.

\[\mathbb{E}_ {x\sim p_{data}}[-log2] + \mathbb{E}_{x \sim p_g}[-log2] = -log4\]

Eq 4수식에 $p_g=p_{data}$를 대입한 결과입니다.



그리고 $C(G) = V(D^*_G, G)$에서 위의 식을 빼면 다음과 같다. \(C(G) = -log(4) + KL(p_{data}||\frac{p_{data}+p_g}{2})+KL(p_g||\frac{p_{data}+p_g}{2}) \tag{5}\)

Eq 4에서 Eq 5까지의 수식을 자세하게 유도해보겠습니다.
\(\begin{align} C(G) &= \mathbb{E} _{x \sim p _{data}}[log \frac{p _{data}(x)}{p _{data}(x) + p_g(x)}] + \mathbb{E} _{z \sim p_z}[log \frac{p_g(x)}{p _{data}(x)+p_g(x)}] \\ &= -log4 + log4 + \mathbb{E} _{x \sim p _{data}}[log \frac{p _{data}(x)}{p _{data}(x) + p_g(x)}] + \mathbb{E} _{z \sim p_z}[log \frac{p_g(x)}{p _{data}(x)+p_g(x)}] \\ &= -log4 + \mathbb{E} _{x \sim p _{data}}[log2] + \mathbb{E} _{x \sim p _{data}}[log \frac{p _{data}(x)}{p _{data}(x) + p_g(x)}] + \mathbb{E} _{z \sim p_z}[log2] + \mathbb{E} _{z \sim p_z}[log \frac{p_g(x)}{p _{data}(x)+p_g(x)}] \\ &= -log4 + \mathbb{E} _{x \sim p _{data}}[log \frac{2 \cdot p _{data}(x)}{p _{data}(x) + p_g(x)}] + \mathbb{E} _{z \sim p_z}[log \frac{2 \cdot p_g(x)}{p _{data}(x)+p_g(x)}] \end{align}\)

여기서 KL를 적용할 수 있습니다.
$KL(B \Vert A) = \mathbb{E}_{x \sim B} [log \frac{B(x)}{A(x)}]$ 이므로 $A$, $B$를 각각 $p_g$, $p _{data}$라고 한다면 수식을 Eq 5 처럼 바꿀 수 있습니다.
\(\begin{align} C(G) &= -log4 + \mathbb{E} _{x \sim p _{data}}[log \frac{2 \cdot p _{data}(x)}{p _{data}(x) + p_g(x)}] + \mathbb{E} _{z \sim p_z}[log \frac{2 \cdot p_g(x)}{p _{data}(x)+p_g(x)}] \\ &= -log(4) + KL(p _{data}\Vert \frac{p _{data}+p_g}{2})+KL(p_g \Vert \frac{p _{data}+p_g}{2}) \end{align}\)


여기서 KL은 Kullback-Leibler divergence이다. 우리는 수식에서 모델의 분포와 데이터 생성과 과정 사이의 Jenson-Shanon의 차이를 인식한다.

KLD(Kullback-Leibler divergence) KLD는 두 확률분포의 차이를 계산할 수 있는 함수로 확률분포 $A$와 확률분포 $B$가 있을 경우 두 분포의 차이는 아래와 같습니다.
$$ D_{KL}(B \| A) = \mathbb{E} _{x \sim B}[log \frac{B(x)}{A(x)}] = \sum \limits _{x} B(x)log \frac{B(x)}{A(x)} $$

참고
- 순록킴님의 초보를 위한 정보이론 안내서 - KL divergence 쉽게 보기]
- Hyeongmin Lee님의 [Kullback-Leibler Divergence & Jenson-Shanon Divergence]

JSD(Jenson-Shanon Divergence) JSD는 두 확률분포 간의 유사성을 측정하는 방법으로 KLD와 유사해보이나 가장 큰 차이는 대칭성입니다. $KL(A\|B) \neq KL(B\|A)$ 이지만 $JSD(A, B) = JSD(B, A)$가 가능해 두 분포 사이 거리 개념으로 사용할 수 있는 것이 가능합니다.



\[C(G) = -log(4) + 2 \cdot JSD(p_{data}||p_g)\]

Eq5인 $C(G) = -log(4) + KL(p _{data}\Vert \frac{p _{data}+p_g}{2})+KL(p_g \Vert \frac{p _{data}+p_g}{2})$에 JSD를 적용해 식을 유도할 수 있습니다.
$JSD(A \Vert B) = \frac{1}{2}KL(A \Vert \frac{A+B}{2}) + \frac{1}{2} KL(B \Vert \frac{A+B}{2})$이므로 $p _{data}$를 A로, $p_g$를 B로 치환한다면 $C(G) = -log(4) + 2 \cdot JSD(p _{data}||p_g)$로 식이 변형됩니다.


두 분포 사이의 Jenson-Shanon divergence는 항상 음의 값이 아니며 두 분포가 같은 때만 0의 값을 가지기 떄문에 $C^* =-log(4)$가 C(G)의 global minimum 값이고 유일하게 $p_g=p_{data}$일 때 데이터 생성 과정을 완벽하게 복제하는 생성모델이라는 것을 보여주었다.

JSD는 $p_g$와 $p_{data}$가 일치할 때 0의 값을 가지며 그 외에는 양수 값을 가지기 때문에 C(G)의 global minimum 값은 $p_g=p_{data}$일 때 $-log4$임을 증명했습니다.

4.2 Convergence of Algorithm 1

이 증명 부분은 Jaejun Yoo님의 초짜 대학원생 입장에서 이해하는 Generative Adversarial Nets(2)의 글을 읽고 쓸 수 있었습니다. 위 글과 같이 읽어보시는 걸 추천드립니다!

Proposition 2. Algorithm 1의 각 단계에서 판별 모델은 최적의 주어진 $G$에 도달할 수 있도록 허용되고 아래의 수식으로 $p_g$가 업데이트될수록 $p_g$는 $p_{data}$에 수렴한다.

\[\mathbb{E} _{x \sim p _{data}}[log D^*_G(x)] + \mathbb{E} _{x \sim p_g}[log(1-D^ *_G(x))]\]

proof. $V(G, D) = U(p_g, D)$를 $p_g$의 함수로 간주한다. $U(p_g, D)$는 $p_g$에서 볼록하다.

$U(p_g, D) = V(G, D) = \int_x p_{data}(x)log(D) + p_glog(1-D)dx$ 로 Eq3과 같으며 Theorm 1을 통해 수식이 $p_g$에 대해 선형함수로 볼록 함수(선형이므로 오목함수 또한 가능)임을 알 수 있습니다.



볼록 함수(convex function)의 supremum(상한)의 subderivatives(하방미분)은 함수의 최대값이 되는 지점의 subderivative를 포함한다. 만약 $f(x) = sup_{\alpha \in \mathcal{A}}f_ \alpha(x)$이고 모든 $f_\alpha(x)$가 모든 $\alpha$에 대해 $x$에서 볼록하다면, $\beta = arg sup_{\alpha \in \mathcal{A}}f_\alpha(x)$일 때 $\partial f_\beta(x) \in \partial$이다.

수식의 변수들이 어색하니 저희에게 해당하는 값으로 바꿔보겠습니다.
$x$ = $p_g$
$\alpha$ = $D$
$\partial$ = subderivative(하방미분)

$f(x) = sup_{\alpha \in \mathcal{A}}f_ \alpha(x)$이고 모든 $f_\alpha(x)$가 모든 $\alpha$에 대해 $x$에서 볼록하다
$\Rightarrow f(p_g) = sup_{D \in \mathcal{D}} f_D(p_g)$이고 모든 $f_D(p_g)$가 모든 $D$에 대해 $p_g$에 대해 볼록하다
위에서 말한 $f(x)$, 즉 $U(p_g, D)$가 ${0}$이 아닌 $D$의 공간에서 $p_g$에 대해 볼록하다는 것을 수식으로 나타낸 것입니다.

$\beta = arg sup_{\alpha \in \mathcal{A}}f_\alpha(x)$일 때 $\partial f_ {\beta}(x) \in \partial$이다.
$\Rightarrow D^* = argsup_{D \in \mathcal{D}}f_D(p_g)$일 때 $\partial f_ { D^* }(p_g) = \partial$이다.
최적의 판별모델 상태인 $D^*$의 subderivative 값이 $U(p_g, D)$의 subderivatives에 포함된다는 것을 수식으로 나타낸 것입니다.

정리하면 $U(p_g, D)$가 $p_g$에 대해서 볼록함수라면 최적의 판별 모델인 $D^ *$의 subderivative 값이 $U(p_g, D)$의 subderivatives에 포함된다. 입니다.

subderivative(하방미분) 하방미분은 미분의 확장 개념입니다. 미분계수와 같이 하나의 숫자로 값이 나오지 않으며 하방미분계수는 점의 집합입니다.
한 점의 하방미분은 해당 점에서 그래프의 모든 접선의 기울기 집합입니다. 다만 함수가 볼록하다는 전제가 필요합니다.
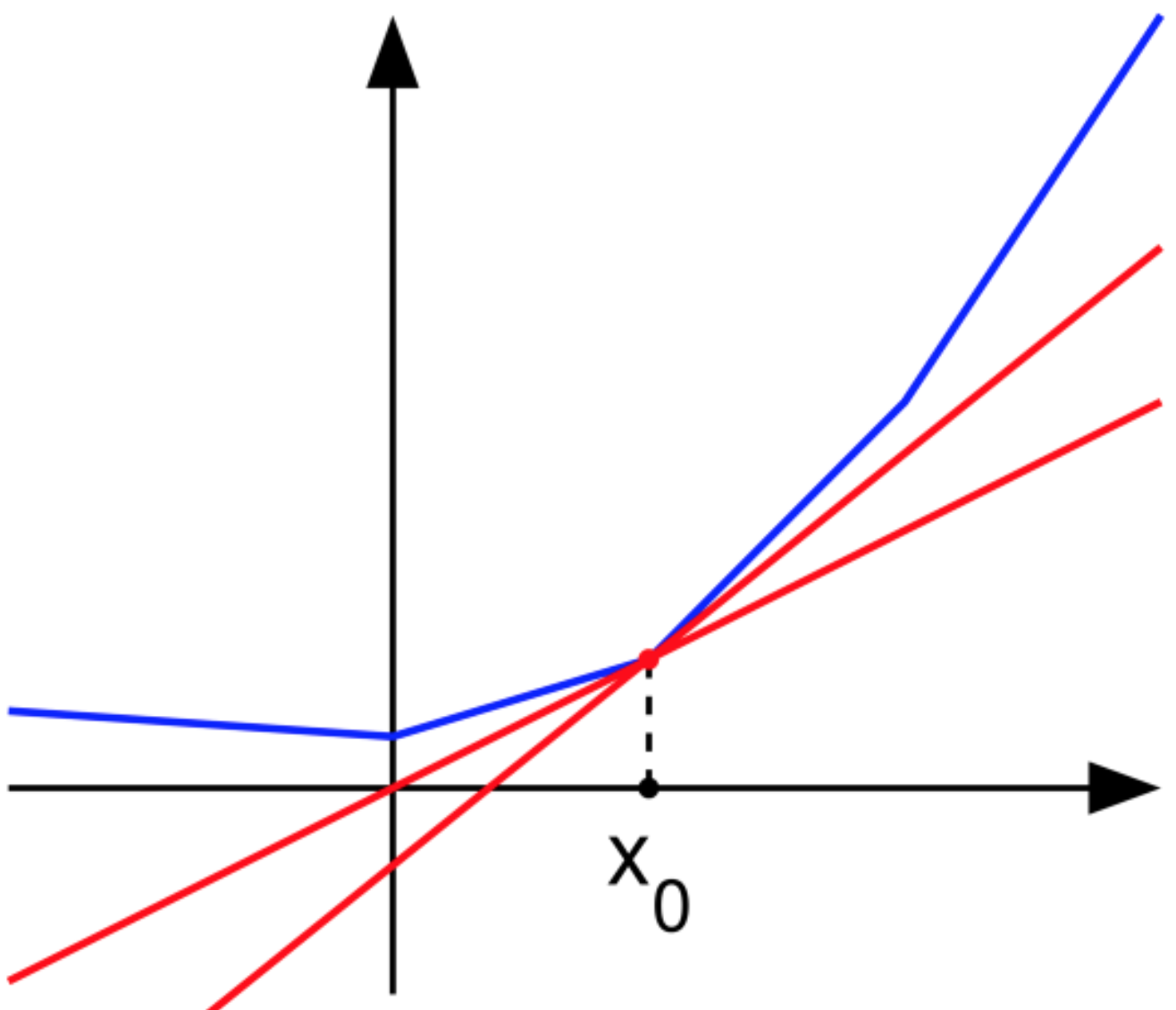
그림에서 빨간 선들의 기울기 값이 하방미분계수의 일부분입니다. $x_0$에 접하는 모든 직선의 기울기 값들이 하방미분계수 집합이 됩니다. 기울기 값들은 $x_0$ 좌측은 기울부터 $x_0$ 우측의 기울기 사이의 값들일 것이며 구간으로 나타낼 수 있습니다.
좌측 기울이가 $a = \lim\limits_{x \to x_0^-} \frac{f(x)-f(x_0)}{x-x_0}$이고 우측 기울기가 $b = \lim\limits_{x \to x_0^+} \frac{f(x)-f(x_0)}{x-x_0}$ 이므로 닫힌 구간 $[a, b]$가 $x_0$에서의 하방미분계수입니다.

참고
- Z Singer님의 Beyond the Derivative-Subderivatives
- 위키백과의 하방미분



$sup_DU(p_g, D)$는 Thm 1에서 증명된 것과 같이 고유한 최적값으로 $p_g$에서 볼록하다. 따라서 $p_g$가 충분히 작은 단위로 업데이트된다면 $p_g$는 $p_x$로 수렴하며 증명을 마무리한다.

Thm1 에서 $p_g$에 대해 $U(p_g, D)$가 볼록함수인 것과 $U(p_g, D)$에 대해 고유한 최적값으로 $-log4$를 가지는 것을 증명했습니다.
따라서 $f(x) = U(p_g, D)$가 볼록하므로 최적의 판별모델 상태 $\beta = D^*$에서 $p_g$의 최적값인 $-log4$를 가질 수 있다 할 수 있습니다.
조금씩 $p_g$를 업데이트한다면 고유한 최적값으로 $p_g$를 업데이트할 수 있다는 것을 증명했습니다:)


실제로 적대적 신경망은 $G(z;\theta_g)$ 함수를 통해 제한된 $p_g$ 분포를 나타내며 우리는 $p_g$ 자체보다는 $\theta_g$를 최적화한다. $G$를 정의하기 위해 다층 퍼셉트론을 사용하는 것은 매개 변수 공간에 여러 임계점을 도입한다. 그러나 실제로 다층 퍼셉트론의 우수한 성능을 이론적 보장이 없음에도 불구하고 사용하기에 합리적인 모델임을 시사한다.

4.Theorical Results에서는 $G$의 분포인 $p_g$를 사용하여 식들을 증명했습니다. 하지만 실제로 모델을 학습할 때는 모델의 분포가 아닌 모델의 파라미터인 $\theta_g$를 최적화합니다. 다층 퍼셉트론인 $G$의 파라미터를 학습할 때의 문제점들이 분명 존재하지만 이론 증명에서는 이 문제점들을 직접 증명하지는 않았습니다.

파라미터 학습의 문제점을 증명하지 않았기에 이론적 보장은 없으나 테스트 결과가 합리적으로 받아드릴 수 있는 만큼 괜찮은 모델임을 설명하기 위해 추가로 적힌 부분인 것 같습니다.

5. Experiments

MNIST, TFD(Toronto Face Database), CIFAR-10을 포함한 데이터셋을 이용해 적대적 네트워크를 학습했다. 생성 모델 네트워크는 rectifier linear activation, sigmoid activation을 섞어 사용했으며 판별 모델 네트워크는 maxout activation을 사용했다. Dropout은 판별 모델 네트워크에 적용되었다. 노이즈는 생성 모델 네트워크의 입력으로 사용했다.

$G$로 생성된 결과 이미지에 Gaussian Parzen Window를 사용해 $p_g$ 안에 테스트 데이터 셋의 확률을 추정하고 이 분포에서 log-likelihood를 확인한다. Gaussian의 매개변수 $\sigma$는 validation 셋에서 교차검증을 통해 얻은 값이다.


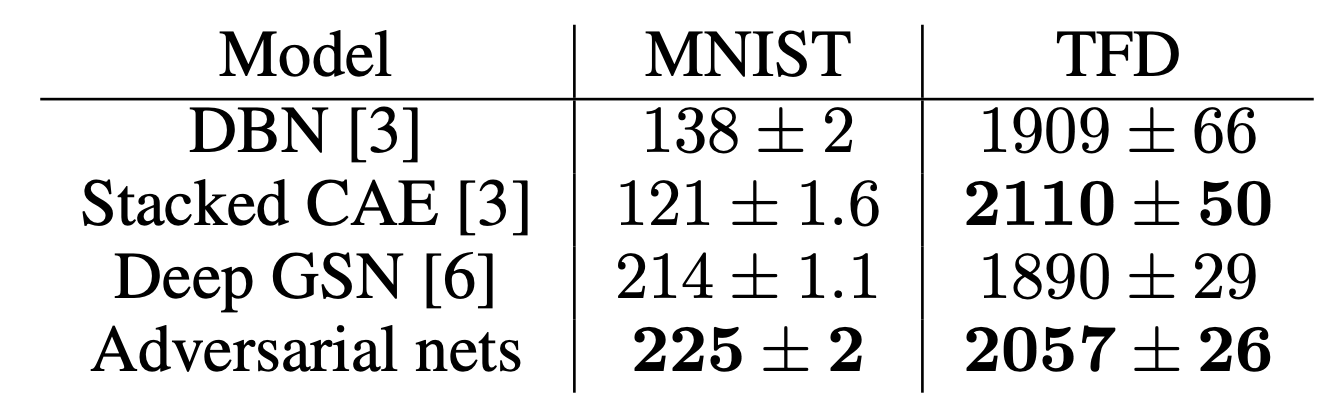table1 Table 1: Parzen window 기반의 log-likelihood 추정치.



figure2 Figure 2: 모델에서 얻어진 이미지들을 시각화한 것이다. 가장 오른쪽 열은 모델이 학습 데이터셋을 기억하지 않았음을 보여주기 위해 학습 데이터셋에서 가장 유사한 이웃 이미지를 보여준다. 이미지들은 좋은 이미지들만 추출한 것이 아닌 공정한 무작위 추출로 추출된 이미지들이다. a)MNIST b)TFD c)CIFAR-10(fully connected model) d)CIFAR-10(convolutional discriminator and deconvolutional generator)



figure3 Figure 3: 숫자들은 모델의 z공간에서 선형 보간을 통해 얻어졌다.

선형 보간(linear interpolation) interpolation(보간)은 점과 점 사이의 값을 추정하는 것을 말합니다. 이 중 linear interpolation은 1차원 직선 상에서 이루어지는 보간법입니다. 2차원으로 확장한 경우 bilinear interpolation(이중 선형 보간법), 3차원으로 확장한 경우 trilinear interpolation(삼중 선형 보간법)이 있습니다.

참고
- 위키백과의 선형보간법
- 다크 프로그래머님의 선형보간법(linear, bilinear, trilinear interpolation)

6. Advantages and disadventages

이 새로운 프레임워크는 이전 모델링 프레임워크에 비해 장단덤이 있다. 단점은 $p_g(x)$의 명시적인 정해진 내용을 출력하는 것이 아닌 것과 학습과정에서 $D$가 학습하는 동안 $G$와 잘 동기화되어야 한다는 것이다(특히 $G$가 $p_{data}$를 모델링하기에 충분한 다양성을 갖기 위해 너무 많은 $z$ 값을 동일한 $x$ 값으로 축소하는 "the Helvetica scenario"를 피하기 위해 $D$를 업데이트하지 않고 $G$를 너무 많이 훈련해서는 안된다.

Helvetica scenario 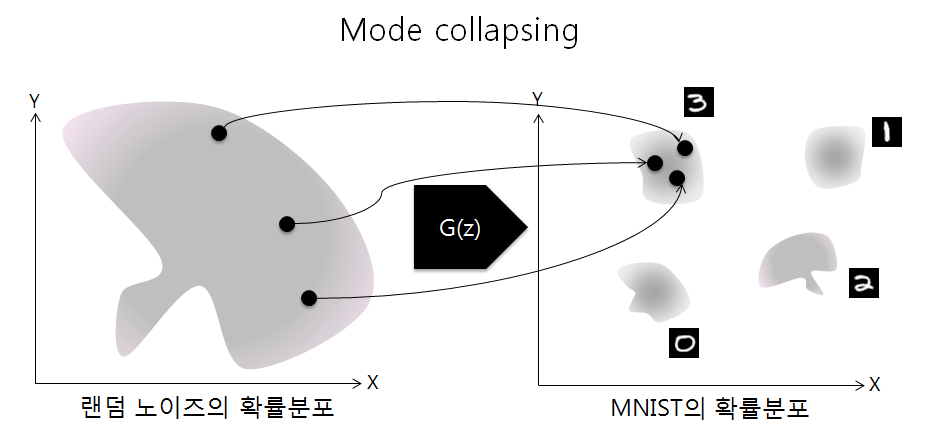Helvetica scenario 또는 Model collapse라 불리는 현상은 생성 모델($G$)이 판별 모델($D$)에 비해 학습 정도가 높아 생성 모델이 특정 클래스만 생성하는 경우를 말합니다.
예시로 $D$의 학습이 아직 불안정해 $G$가 생성한 숫자 2는 $D$가 학습 데이터에서 온 데이터가 아니라 판단하고 숫자 3은 학습 데이터에서 온 데이터라 판단한 경우 $G$는 $D$를 속이기 위해 이미 속이는 것을 성공한 숫자 3만을 생성하게 됩니다.

참고
- Learn.AI 님의 GAN이 풀어야 할 과제들

7. Conclusions and future work

이 프레임워크는 수많은 간단한 확장들을 허용한다.

  1. 조건부 생성(conditional generative) 모델 $p(x|c)$는 $G$와 $D$ 모두에 조건 $c$를 입력함으로써 얻을 수 있다.

  2. 학습된 근사 추론(approximate inference)은 주어진 $x$로 $z$를 예측하도록 보조 네트워크(Auxiliary network)를 훈련함으로써 수행될 수 있다. 이는 wake-sleep 알고리즘에 의해 훈련된 추론 네트워크와 유사하지만, 생성 네트워크가 학습을 마친 후 고정된 상태에 대해 추론 네트워크를 학습할 수 있다는 장점이 있다.

  3. 매개 변수를 공유하는 조건부 모델들을 학습시킴으로써 $S$가 $x$의 지수의 부분 집합인 모든 조건부 $p(x_S | x_{\not S})$를 근사적으로 모델링할 수 있다. 본질적으로 결정론적 MP-DBM의 확률적 확장을 구현하기 위해 적대적 네트워크를 사용할 수 있다.

  4. 준지도 학습 : 판별 모델 또는 추론 네트워크의 기능은 제한된 라벨링된 데이터를 사용할 수 있을 때 판별 성능을 향상시킬 수 있다.

  5. 효율성 향상 : $G$와 $D$를 더 좋은 알고리즘으로 조정하거나 학습 중에 샘플 $z$에 더 나은 분포로 개선함으로써 훈련을 크게 가속화할 수 있다.

이 논문은 적대적 모델링 프레임워크의 실행 가능성을 입증했으며, 이러한 연구 방향이 유용할 수 있음을 시사한다.

다음 논문 코드글에서 논문을 코드로 구현해보겠습니다.
코드 글에서 뵙겠습니다:)